题目内容
如果一个三角形的两边长分别是5和7，那么第三边上的中线的长度m的取值范围是 ；原三角形的最短边长a的取值范围是 ．
考点：全等三角形的判定与性质,三角形三边关系
专题：
分析：延长AD至E，使AD=DE，构建全等三角形：△CDA≌△BDE．则利用全等三角形的对应边相等和△ABE的三边关系来求AD的取值范围；
根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边，即可求解．
根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边，即可求解．
解答：
解：如图所示，AB=5，AC=7，
设BC=2a，AD=x，
延长AD至E，使AD=DE，
在△CDA与△BDE中，
，
∴△CDA≌△BDE（SAS），
∴AE=2x，BE=AC=7，
在△ABE中，BE-AB＜AE＜AB+BE，即7-5＜2x＜7+5，
∴1＜x＜6．
根据三角形的三边关系和a是最短边知：7-5＜a＜5，即2＜a＜5．
故答案为：1＜x＜6；2＜a＜5．
解：如图所示，AB=5，AC=7，设BC=2a，AD=x，
延长AD至E，使AD=DE，
在△CDA与△BDE中，
|
∴△CDA≌△BDE（SAS），
∴AE=2x，BE=AC=7，
在△ABE中，BE-AB＜AE＜AB+BE，即7-5＜2x＜7+5，
∴1＜x＜6．
根据三角形的三边关系和a是最短边知：7-5＜a＜5，即2＜a＜5．
故答案为：1＜x＜6；2＜a＜5．
点评：本题考查了全等三角形的判定与性质和三角形的三边关系．有关三角形的中线问题，通常要倍数延长三角形的中线，把三角形的一边变换到与另一边和中线的两倍组成三角形，再根据三角形三边关系定理列出不等式，然后解不等式即可．
练习册系列答案
相关题目
一商标图案如图阴影部分，长方形ABCD中AB=6cm，BC=3cm，以点A为圆心，AD为半径作圆与BA的延长线相交于点F，则商标图案的面积为
已知AC=BD，∠E=∠F，BE∥DF，求证：BE=DF．
一个涵洞成抛物线形，它的截面如图，当水面宽AB=1.6 米时，涵洞顶点与水面的距离为2.4m．涵洞所在抛物线的解析式是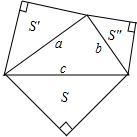
如图，以直角三角形的三边为斜边向形外作等腰直角三角形，以直角边a，b为斜边的等腰直角三角形面积记为S′和S″，直角三角形的斜边长c为8，则S′+S″=