题目内容
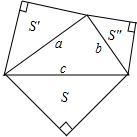 如图,以直角三角形的三边为斜边向形外作等腰直角三角形,以直角边a,b为斜边的等腰直角三角形面积记为S′和S″,直角三角形的斜边长c为8,则S′+S″=
如图,以直角三角形的三边为斜边向形外作等腰直角三角形,以直角边a,b为斜边的等腰直角三角形面积记为S′和S″,直角三角形的斜边长c为8,则S′+S″=考点:勾股定理
专题:
分析:先用中间直角三角形的边长表示出三个等腰直角三角形的面积,再根据勾股定理可得:c2=a2+b2,进而可将S′+S″的面积求出.
解答:解:由勾股定理可得c2=a2+b2,
S=
c×
c×
=
c2,
S′=
a×
a×
=
a2,
S″=
b×
b×
=
b2,
S′+S″
=
a2+
b2
=
(a2+b2)=
c2
=
×8×8
=16.
故答案为:16.
S=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
S′=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
S″=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
S′+S″
=
| 1 |
| 4 |
| 1 |
| 4 |
=
| 1 |
| 4 |
| 1 |
| 4 |
=
| 1 |
| 4 |
=16.
故答案为:16.
点评:本题主要是考查勾股定理的应用,比较简单.注意:以直角三角形的两条直角边为斜边的两个等腰直角三角形的面积的和等于以斜边为斜边的等腰直角三角形的面积;等腰直角三角形的斜边是直角边的
倍.
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
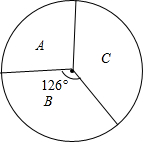 某校对1500名在校学生进行每周上网的情况调查,A为每天上网的学生,B为从不上网的学生,C为偶尔上网的学生,如扇形统计图所示,根据注释,解答以下问题:
某校对1500名在校学生进行每周上网的情况调查,A为每天上网的学生,B为从不上网的学生,C为偶尔上网的学生,如扇形统计图所示,根据注释,解答以下问题: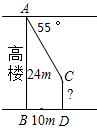 如图,王师傅在楼顶上的点A处测得楼前一棵树CD的顶端C的俯角为55°,又知水平距离BD=10m,楼高AB=24m,则树高CD等于
如图,王师傅在楼顶上的点A处测得楼前一棵树CD的顶端C的俯角为55°,又知水平距离BD=10m,楼高AB=24m,则树高CD等于