题目内容
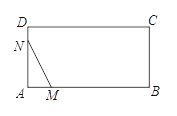
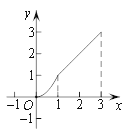
【题目】某景区平面图如图1所示，
为边界上的点.已知边界
是一段抛物线，其余边界均为线段，且
，抛物线顶点
到
的距离
.以所在直线为
轴，
所在直线为
轴，建立平面直角坐标系.
求边界所在抛物线的解析式;
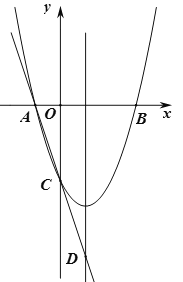
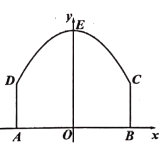
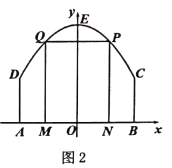
如图2，该景区管理处欲在区域
内围成一个矩形
场地，使得点
在边界上，点
在边界上，试确定点
的位置，使得矩形的周长最大，并求出最大周长.
【答案】（1）
（
）；（2）点
与点
重合，
取最大值
.
【解析】
（1）首先由题意得出
，然后代入抛物线解析式，即可得解；
（2）首先设点的坐标为
，矩形
的周长为，然后根据坐标与周长构建二次函数，即可求的最大值.
由题意得，，且
为抛物线的顶点，
则设抛物线的解析式为
，
代入
得:
，解得
所以边界
所在抛物线的解析式是（）
设点的坐标为，矩形的周长为.则，
，
矩形的周长，
化简得
，
当
时，取最大值.此时点与点重合.
练习册系列答案
阅读快车系列答案
相关题目
