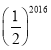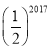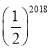题目内容
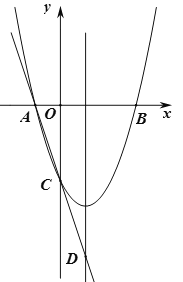
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 交二次函数图象的对称轴于点
交二次函数图象的对称轴于点![]() ,若点C为
,若点C为![]() 的中点.
的中点.
(1)求![]() 的值;
的值;
(2)若二次函数图象上有一点![]() ,使得
,使得![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)对于(2)中的![]() 点,在二次函数图象上是否存在点
点,在二次函数图象上是否存在点![]() ,使得
,使得![]() ∽
∽![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)不存在,理由见解析.
;(3)不存在,理由见解析.
【解析】
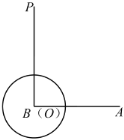
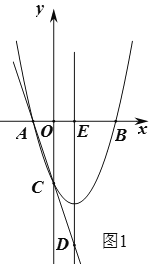
(1)设对称轴与![]() 轴交于点
轴交于点![]() ,如图1,易求出抛物线的对称轴,可得OE的长,然后根据平行线分线段成比例定理可得OA的长,进而可得点A的坐标,再把点A的坐标代入抛物线解析式即可求出m的值;
,如图1,易求出抛物线的对称轴,可得OE的长,然后根据平行线分线段成比例定理可得OA的长,进而可得点A的坐标,再把点A的坐标代入抛物线解析式即可求出m的值;
(2)设点Q的横坐标为n,当点![]() 在
在![]() 轴上方时,过点Q作QH⊥x轴于点H,利用
轴上方时,过点Q作QH⊥x轴于点H,利用![]() 可得关于n的方程,解方程即可求出n的值,进而可得点Q坐标;当点
可得关于n的方程,解方程即可求出n的值,进而可得点Q坐标;当点![]() 在
在![]() 轴下方时,注意到
轴下方时,注意到![]() ,所以点
,所以点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,由此可得点Q坐标;
对称,由此可得点Q坐标;
(3)当点![]() 为x轴上方的点时,若存在点P,可先求出直线BQ的解析式,由BP⊥BQ可求得直线BP的解析式,然后联立直线BP和抛物线的解析式即可求出点P的坐标,再计算此时两个三角形的两组对应边是否成比例即可判断点P是否满足条件;当点Q取另外一种情况的坐标时,再按照同样的方法计算判断即可.
为x轴上方的点时,若存在点P,可先求出直线BQ的解析式,由BP⊥BQ可求得直线BP的解析式,然后联立直线BP和抛物线的解析式即可求出点P的坐标,再计算此时两个三角形的两组对应边是否成比例即可判断点P是否满足条件;当点Q取另外一种情况的坐标时,再按照同样的方法计算判断即可.
解:(1)设抛物线的对称轴与![]() 轴交于点
轴交于点![]() ,如图1,∴
,如图1,∴![]() 轴
轴![]() ,∴
,∴![]() ,
,
∵抛物线的对称轴是直线![]() ,∴OE=1,∴
,∴OE=1,∴![]() ,∴
,∴![]()
∴将点![]() 代入函数表达式得:
代入函数表达式得:![]() ,∴
,∴![]() ;
;
(2)设![]() ,
,
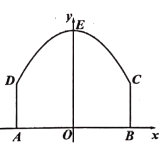
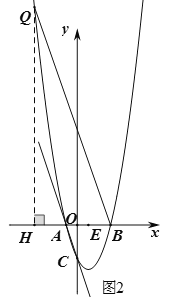
①点![]() 在
在![]() 轴上方时,
轴上方时,![]() ,如图2,过点Q作QH⊥x轴于点H,∵
,如图2,过点Q作QH⊥x轴于点H,∵![]() ,∴
,∴![]() ,解得:
,解得:![]() 或
或![]() (舍),∴
(舍),∴![]() ;
;
②点![]() 在
在![]() 轴下方时,∵OA=1,OC=3,∴
轴下方时,∵OA=1,OC=3,∴![]() ,∵
,∵![]() ,∴点
,∴点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,∴
对称,∴![]() ;
;
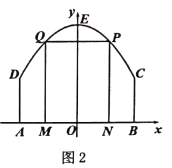
(3)①当点![]() 为
为![]() 时,若存在点P,使
时,若存在点P,使![]() ∽
∽![]() ,则∠PBQ=∠COA=90°,
,则∠PBQ=∠COA=90°,
由B(3,0)、Q![]() 可得,直线BQ的解析式为:
可得,直线BQ的解析式为:![]() ,所以直线PB的解析式为:
,所以直线PB的解析式为:![]() ,
,
联立方程组: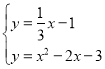 ,解得:
,解得: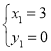 ,
,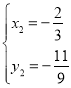 ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 不存在;
不存在;
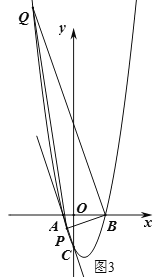
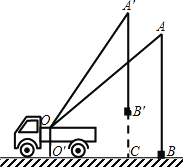
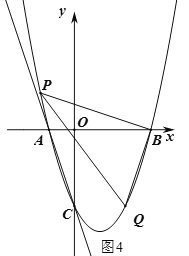
②当点![]() 为
为![]() 时,如图4,由B(3,0)、Q
时,如图4,由B(3,0)、Q![]() 可得,直线BQ的解析式为:
可得,直线BQ的解析式为:![]() ,所以直线PB的解析式为:
,所以直线PB的解析式为:![]() ,
,
联立方程组: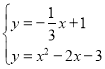 ,解得:
,解得: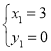 ,
,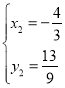 ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 不存在.
不存在.
综上所述,不存在满足条件的点![]() ,使
,使![]() ∽
∽![]() .
.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案