题目内容
【题目】如图，
是
的外接圆，
，点
是外一点，
，
，则线段
的最大值为（ ）
A.9B.4.5C.
D.
【答案】C
【解析】
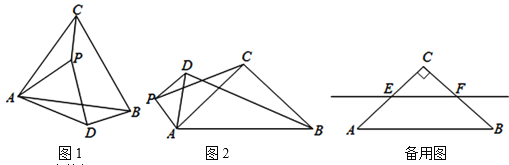
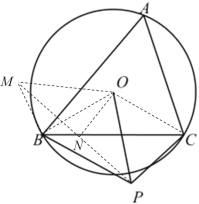
连接OB、OC，如图，则△OBC是顶角为120°的等腰三角形，将△OPC绕点O顺时针旋转120°到△OMB的位置，连接MP，则∠POM=120°，MB=PC=3，OM=OP，根据等腰三角形的性质和锐角三角函数可得 
，于是求OP的最大值转化为求PM的最大值，因为
，所以当P、B、M三点共线时，PM最大，据此求解即可.
解：连接OB、OC，如图，则OB=OC，∠BOC=2∠A=120°，将△OPC绕点O顺时针旋转120°到△OMB的位置，连接MP，则∠POM=120°，MB=PC=3，OM=OP，
过点O作ON⊥PM于点N，则∠MON=60°，MN=
PM，
在直角△MON中，
，∴
，
∴当PM最大时，OP最大，
又因为，所以当P、B、M三点共线时，PM最大，此时PM=3+6=9，
所以OP的最大值是：
.
故选：C.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
