题目内容
 如图,AD⊥CD于点D,BC⊥CD于点C,点E是CD的中点,AE平分∠BAD.求证:BE平分∠ABC.
如图,AD⊥CD于点D,BC⊥CD于点C,点E是CD的中点,AE平分∠BAD.求证:BE平分∠ABC.考点:全等三角形的判定与性质
专题:证明题
分析:作EM⊥AB,垂足为M,构造全等三角形,可得DE=EM,结合点E是CD的中点和AE平分∠BAD,可证得∠MBE=∠CBE,可得结论.
解答:
证明:
作EM⊥AB,垂足为M,
∵∠D=∠AME=90°,AE=AE,∠DAE=∠MAE,
在△ADE和△AME中
∴△ADE≌△AME,
∴DE=EM,
∵DE=EC,
∴EM=EC,
∵EM⊥BE,EC⊥BC,
∴∠MBE=∠CBE,
∴BE平分∠ABC.

证明:
作EM⊥AB,垂足为M,
∵∠D=∠AME=90°,AE=AE,∠DAE=∠MAE,
在△ADE和△AME中
|
∴△ADE≌△AME,
∴DE=EM,
∵DE=EC,
∴EM=EC,
∵EM⊥BE,EC⊥BC,
∴∠MBE=∠CBE,
∴BE平分∠ABC.
点评:本题主要考查三角形全等的判定及性质,解题的关键是构造三角形全等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
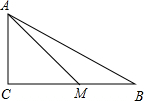 已知在△ABC中,∠C=90°,M在BC上,若AB=17,AM=10,BM=9,求AC、MC的长.
已知在△ABC中,∠C=90°,M在BC上,若AB=17,AM=10,BM=9,求AC、MC的长. 已知如图,在△ABC中,AB=2AC,AD是∠BAC的角平分线,且AD=BD.求证:∠ADB=2∠ADC.
已知如图,在△ABC中,AB=2AC,AD是∠BAC的角平分线,且AD=BD.求证:∠ADB=2∠ADC. 如图所示,∠1=∠2,∠3=∠4,AC、BD相交于点E,求证:AC是线段BD的垂直平分线.
如图所示,∠1=∠2,∠3=∠4,AC、BD相交于点E,求证:AC是线段BD的垂直平分线.