题目内容

4．抛物线y=$\frac{1}{2}$x2-3与y轴的交点为（0，-3）．

分析 把x=0代入抛物线y=$\frac{1}{2}$x2-3，即得抛物线y=$\frac{1}{2}$x2-3与y轴的交点．

解答 解：∵当x=0时，抛物线y=$\frac{1}{2}$x2-3与y轴相交，
∴把x=0代入y=$\frac{1}{2}$x2-3，求得y=-3，
∴抛物线y=$\frac{1}{2}$x2-3与y轴的交点坐标为（0，-3）．
故答案为（0，-3）．

点评 本题考查了二次函数图象上点的坐标特征，比较简单，掌握y轴上点的横坐标为0是解题的关键．

练习册系列答案
相关题目
14．若（a-2）x|a|-1-3=6是关于x的一元一次方程，则a的值为-2．
15．如图，已知抛物线y=$\frac{1}{2}$x2+ax+4a与x轴交于点A、B，与y轴负半轴交于点C且OB=OC，点P为抛物线上的一个动点，且点P位于x轴下方，点P与点C不重合．
（1）求该抛物线的解析式；
（2）若△PAC的面积为$\frac{1}{2}$，求点P的坐标；
（3）若以A、B、C、P为顶点的四边形面积记作S，则S取何值时，对应的点P有且只有2个？
12．下列说法中不正确的是（　　）
A．所有的有理数都有相反数
B．数轴上和原点的距离相等的两个点所表示的数一定互为相反数
C．正数和负数互为相反数
D．在一个有理数前添一个“-”号，就得到它的相反数
19．在△ABC中，若tanA=1，sinB=$\frac{{\sqrt{2}}}{2}$，关于△ABC的形状说法最准确的是（　　）
A．是等腰三角形B．是等腰直角三角形
C．是直角三角形D．是一般锐角三角形
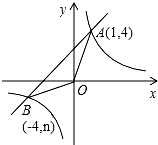9．已知：如图，反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=x+b的图象交于点A（1，4），点B（-4，n）．
（1）求一次函数和反比例函数的解析式；
（2）求△OAB的面积；
（3）根据图象，试比较y1，y2的大小．
16．计算
（1）12-（-18）+（-7）-15
（2）$（{-4\frac{7}{8}}）-（{-5\frac{1}{2}}）+（{-4\frac{1}{4}}）-（{+3\frac{3}{8}}）$
（3）$（{-\frac{3}{4}}）×（{-1\frac{1}{2}}）÷（{-2\frac{1}{4}}）$
（4）-9×（-11）÷3÷（-3）
（5）$42×（{-\frac{2}{3}}）+（{-\frac{3}{4}}）÷（{-0.25}）$
（6）$-|{-\frac{2}{3}}|-|{-\frac{1}{2}×\frac{2}{3}}|-|{\frac{1}{3}-\frac{1}{4}}|-|{-3}|$
（7）${（{-5}）^3}-3×{（{-\frac{1}{2}}）^4}$     
（8）$\frac{6}{5}×（{-\frac{2}{3}}）+（{-\frac{6}{5}}）×（{-\frac{17}{3}}）$
（9）$（{\frac{1}{4}+\frac{1}{6}-\frac{1}{2}}）×12$
（10）（-2）3+（-3）×[（-4）2+2]-（-3）2÷（-2）
13．周末，张华骑自行车从家里出发到野外郊游，从家出发1小时后到达甲地，游玩一段时间按原速前往乙地，张华离家2小时20分钟后，妈妈驾车沿相同路线前往乙地，如图是他们离家的路程y（单位：千米）与张华离家时间x（单位：小时）的函数图象，已知妈妈驾车的速度是张华骑车速度的3倍．
（1）求张华和妈妈的速度分别是多少？
（2）张华从家出发多少小时后被妈妈追上？此时离家多远？
（3）若妈妈比张华早16分钟到达乙地，求从家到乙地的路程．
14．已知a2+bc=14，b2-2bc=-6，则3a2+4b2-5bc的值是（　　）
A．8B．12C．16D．18

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网