题目内容
14．已知三角形的三边长分别为4，a，8，那么a的取值范围是（ ）| A． | 4＜a＜8 | B． | 4＜a＜12 | C． | 1＜a＜12 | D． | 4＜a＜6 |
分析 根据三角形两边之和大于第三边，三角形的两边差小于第三边可得8-4＜a＜8+4，再解不等式即可．
解答 解：根据三角形的三边关系可得：8-4＜a＜8+4，
即：4＜a＜12．
故选：B．
点评 此题主要考查了三角形的三边关系，关键是掌握第三边的范围是：大于已知的两边的差，而小于两边的和．
练习册系列答案
相关题目
5．
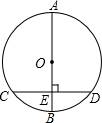如图，AB为⊙O的直径，弦CD垂直平分半径OB，垂足为E，CD=6cm，则直径AB的长是（ ）
如图，AB为⊙O的直径，弦CD垂直平分半径OB，垂足为E，CD=6cm，则直径AB的长是（ ）| A． | 10cm | B． | 3$\sqrt{2}$cm | C． | 4$\sqrt{2}$cm | D． | 4$\sqrt{3}$cm |
9．计算：1002-2×100×99+992=（ ）
| A． | 0 | B． | 1 | C． | -1 | D． | 39601 |
6．
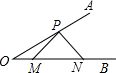如图，已知∠AOB=30°，点P在边OA上，OP=4，点M，N在边OB上，PM=PN，且∠MPN=90°，则ON=（ ）
如图，已知∠AOB=30°，点P在边OA上，OP=4，点M，N在边OB上，PM=PN，且∠MPN=90°，则ON=（ ）| A． | 8 | B． | 6 | C． | 2$\sqrt{3}$+4 | D． | 2$\sqrt{3}$+2 |
3．下列等式成立的是（ ）
| A． | $\sqrt{7}$-$\sqrt{2}$=$\sqrt{5}$ | B． | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | C． | $\sqrt{{2}^{2}+{3}^{2}}$=5 | D． | -$\sqrt{（-5）^{2}}$=5 |