题目内容
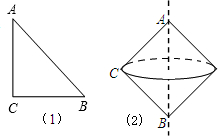 如图(1),在Rt△ABC中,∠ACB=90°,
如图(1),在Rt△ABC中,∠ACB=90°,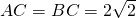 ,
,
(1)若把Rt△ABC绕边AC所在直线旋转一周,求所得几何体的表面积;
(2)如图(2),若绕边AB所在直线旋转一周,则所得几何体的表面积是多少?
解:(1)由题意知,∵在Rt△ABC中,∠ACB=90°,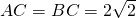 ,
,
∴BA2=CB2+AC2=16,
∴AB=4,
以BC为半径的圆的周长=2π×2 =4
=4 π,底面面积=π(2
π,底面面积=π(2 )2=8π,
)2=8π,
得到的圆锥的侧面面积= ×4
×4 π×4=8
π×4=8 π,
π,
表面积=8 π+8π,
π+8π,
(2)∵Rt△ABC中,∠ACB=90°,AC=BC=2 ,
,
∴AB=4,
∴所得圆锥底面半径为2,
∴几何体的表面积=2×π×2×2 =8
=8 π.
π.
分析:(1)易得此几何体为圆锥,那么表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2.
(2)所得几何体的表面积为2个底面半径为2,母线长为2 的圆锥侧面积的和.
的圆锥侧面积的和.
点评:此题主要考查了圆锥侧面积的计算,关键是利用圆锥的侧面积=底面周长×母线长÷2得出.
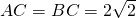 ,
,∴BA2=CB2+AC2=16,
∴AB=4,
以BC为半径的圆的周长=2π×2
 =4
=4 π,底面面积=π(2
π,底面面积=π(2 )2=8π,
)2=8π,得到的圆锥的侧面面积=
 ×4
×4 π×4=8
π×4=8 π,
π,表面积=8
 π+8π,
π+8π,(2)∵Rt△ABC中,∠ACB=90°,AC=BC=2
 ,
,∴AB=4,
∴所得圆锥底面半径为2,
∴几何体的表面积=2×π×2×2
 =8
=8 π.
π.分析:(1)易得此几何体为圆锥,那么表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2.
(2)所得几何体的表面积为2个底面半径为2,母线长为2
 的圆锥侧面积的和.
的圆锥侧面积的和.点评:此题主要考查了圆锥侧面积的计算,关键是利用圆锥的侧面积=底面周长×母线长÷2得出.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
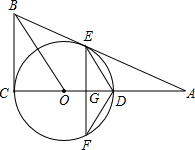 (2012•中江县二模)如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连接BO、ED,且BO∥ED,作弦EF⊥AC于G,连接DF.
(2012•中江县二模)如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连接BO、ED,且BO∥ED,作弦EF⊥AC于G,连接DF.
 如图,已知:在Rt△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D.
如图,已知:在Rt△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D. 如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.
如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.