Question

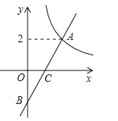
【题目】如图，平面直角坐标系xOy中，一次函数y=kx-k的图象与函数y=(x＞0)的图象交点为A，与y轴交于点B，P是x轴上一点，且△PAB的面积是4，则P的坐标____．

Answer 1

【答案】(3,0)或(-1,0)

【解析】

本题考查一次函数与反比例函数综合问题，需利用待定系数法求解一次函数解析式，继而求解B，C点坐标，因为同时考查动点问题，故需要按照分类讨论方式结合三角形面积公式求解本题．

因为点A在反比例函数上，故将A点纵坐标代入y=，求得A点坐标为(2，2)

又因为点A在一次函数上，故将A(2，2)代入y=kx-k，得k=2，故一次函数为y=2x-2

将x=0代入一次函数，求得B点纵坐标为-2，得B(0，-2)

将y=0代入一次函数，求得C点横坐标为1，得C(1，0)

假设P(x，0)，则PC= ，将△PAB面积拆分为以PC为底边，A，B点纵坐标高度分别为高的△PAC和△PBC

则S△PAB=S△PAC+S△PBC=

求得x=3或-1

所以P(3，0)或(-1，0)

故答案为：（3，0）或（-1，0）