Question

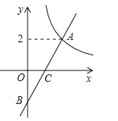
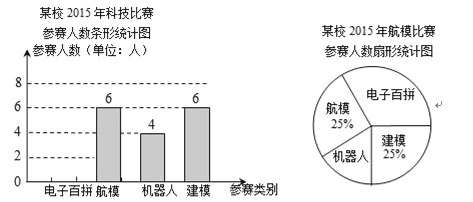
【题目】图1是一种手机自拍杆，杆体从上至下分别由手机夹架、多节套管和可升降支架脚连接而成．使用时通过自由伸缩套管调节自拍杆的长度，同时可以通过调节支架脚使拍摄时更灵活安全．图2是其正面简化示意图，手机（为矩形）与其下方套管连接于点E，E为的中点，，支架脚，与地面平行，．

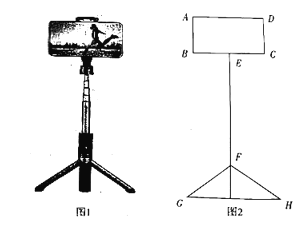
（1）当时，求点E到地面的高度；

（2）若在某环境中拍摄时，调节支架脚使，若，求点G到直线与交点的距离．

（参考数据：，结果精确到）

Answer 1

【答案】（1）点E到地面的高度；（2）点G到直线与交点的距离约为．

【解析】

（1）如图（见解析），先根据平行线的性质得出，再根据等腰三角形的性质、三角形的内角和定理得出，然后根据直角三角形的性质可得FM的长，最后根据线段的和差即可得；

（2）先利用等腰三角形的性质、余弦值求出GH的长，从而确定与交点的位置，如图（见解析），延长AB分别交GF于点P，交GH于点Q，再根据矩形的判定与性质可得MQ的长，从而可得GQ的长，然后在中利用余弦值即可得．

（1）如图，设EF与GH的交点为点M

，即

，

在中，

答：点E到地面的高度；

（2）由（1）已知，

（等腰三角形的三线合一）

，即

则依题意，延长AB分别交GF于点P，交GH于点Q，画图如下所示：

四边形ABCD是矩形

，即

，即

又

四边形BEMQ是平行四边形

平行四边形BEMQ是矩形

，点E是BC的中点

在中，，即

解得

答：点G到直线与交点的距离约为．