题目内容
若反比例函数y=
的图象经过点A(x1,y1)和点B(x2,y2),且当0<x1<x2时,y1>y2>0,则m的取值范围是( )
| 1-2m |
| x |
| A、m<0 | ||
| B、m>0 | ||
C、m<
| ||
D、m>
|
考点:反比例函数图象上点的坐标特征
专题:计算题
分析:根据反比例函数的性质由0<x1<x2时,y1>y2>0得到1-2m>0,然后解不等式即可.
解答:解:∵当0<x1<x2时,y1>y2>0,
∴反比例函数图象在第一、三象限,
∴1-2m>0,
∴m<
.
故选C.
∴反比例函数图象在第一、三象限,
∴1-2m>0,
∴m<
| 1 |
| 2 |
故选C.
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了反比例函数的性质.
| k |
| x |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列四个命题中,正确的是( )
| A、一组对边平行,另一组对边相等的四边形是平行四边形 |
| B、一组对边平行,一组对角相等的四边形是平行四边形 |
| C、一组对边相等,一组对角相等的四边形是平行四边形 |
| D、一组对边平行,一组邻角互补的四边形是平行四边形 |
一组数据11,12,13,14,15,16的平均数是( )
| A、13 | B、13.5 |
| C、14 | D、14.5 |
方程
=
的解为( )
| 1 |
| 2x |
| 1 |
| x2+1 |
| A、1 | B、-1 | C、±1 | D、0 |
若关于x的方程(m-2)x2+
x+1=0是一元二次方程,则m的取值范围是( )
| m |
| A、m≠2 | B、m>0 |
| C、m≠2且m≥0 | D、m为任何实数 |
小明在解方程x2-x=0时,只得出一个根是1,则被漏掉的一个根是( )
| A、x=0 | B、x=1 |
| C、x=2 | D、x=3 |
 如图,在?ABCD中,对角线AC,BD交于点O,将△AOD平移至△BEC的位置,连结0E,则图中平行四边形的个数为( )
如图,在?ABCD中,对角线AC,BD交于点O,将△AOD平移至△BEC的位置,连结0E,则图中平行四边形的个数为( )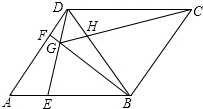 如图,在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG.
如图,在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG.