题目内容
14.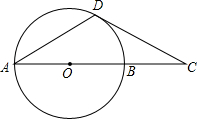 如图,⊙O的直径AB=10,切线DC与AB的延长线交于点C,D为切点,若∠A=30°,则BC=5.
如图,⊙O的直径AB=10,切线DC与AB的延长线交于点C,D为切点,若∠A=30°,则BC=5.
分析 连接OD,连接OD,求出OB=OA=OC=5,∠A=∠ADO=30°,∠DOB=∠A+∠ADO=60°,根据切线的性质求出∠ODC=90°,求出OC=2OD=10,即可得出答案.
解答 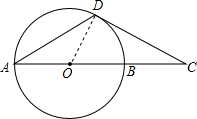 解:如图,连接OD,
解:如图,连接OD,
∵⊙O的直径AB=10,
∴OB=OA=OC=5,
∴∠A=∠ADO,
∵∠A=30°,
∴∠ADO=30°,
∴∠DOB=∠A+∠ADO=60°,
∵CD切⊙O于D,
∴OD⊥DC,
∴∠ODC=90°,
∴∠C=180°-90°-60°=30°,
∴OC=2OD=10,
∴BC=OC-OB=10-5=5.
故答案为:5.
点评 本题考查了切线的性质,等腰三角形的性质,三角形外角性质的应用,能求出∠ODC=90°和∠C=30°是解此题的关键,注意:圆的切线垂直于过切点的半径.

练习册系列答案
相关题目
4.下列图案是轴对称图形不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.已知∠AOB=70°,∠BOC=30°,OM平分AOB,ON平分∠BOC,则∠MON=( )
| A. | 50° | B. | 20° | C. | 20°或50° | D. | 不能确定 |
9.小明同学体考前,进行了7次测试,其测试成绩分别为:48,49,49,46,47,49,46,则这组数据的中位数和众数分别是( )
| A. | 47和49 | B. | 48和49 | C. | 47和46 | D. | 48和46 |
19. 2015年3月全国两会期间,民生活题成为了社会关注的焦点,成都商报为了了解百姓“两会民生活题”的聚焦点,记者随机调查了成都市部分市民,并对调查进行整理,绘制成了如图所示的不完整的统计图表.
2015年3月全国两会期间,民生活题成为了社会关注的焦点,成都商报为了了解百姓“两会民生活题”的聚焦点,记者随机调查了成都市部分市民,并对调查进行整理,绘制成了如图所示的不完整的统计图表.
根据图表中提供的信息可得统计表中m=40,n=100,扇形统计图中D组所占的百分比为25%.
 2015年3月全国两会期间,民生活题成为了社会关注的焦点,成都商报为了了解百姓“两会民生活题”的聚焦点,记者随机调查了成都市部分市民,并对调查进行整理,绘制成了如图所示的不完整的统计图表.
2015年3月全国两会期间,民生活题成为了社会关注的焦点,成都商报为了了解百姓“两会民生活题”的聚焦点,记者随机调查了成都市部分市民,并对调查进行整理,绘制成了如图所示的不完整的统计图表.| 组别 | 焦点话题 | 频数(人数) |
| A | 延迟退休 | 120 |
| B | 汽车尾号限行 | 80 |
| C | 就业养老 | m |
| D | 教育医疗 | n |
| E | 生态环保 | 60 |
3.已知菱形ABCD的边长为5,中心为O,且OA,OB的长是关于x的方程x2+(2m+1)x+m2-4=0的两个实数根,则m的值为( )
| A. | -4 | B. | 2 | C. | -4或2 | D. | 以上都不对 |