题目内容
(1)已知:1+2+3+…+31+32+33=17×33,求1-3+2-6+3-9+4-12+…+31-93+32-96+33-99的值.
(2)已知:x>0,y<0,求|x-y+2|-|y-x-3|的值.
(2)已知:x>0,y<0,求|x-y+2|-|y-x-3|的值.
考点:有理数的混合运算,绝对值
专题:规律型
分析:(1)先将1-3+2-6+3-9+4-12+…+31-93+32-96+33-99变形为-2(1+2+3+…+31+32+33),再进行计算;
(2)根据x、y的取值确定x-y+2和y-x-3的取值,从而去掉绝对值符号化简.
(2)根据x、y的取值确定x-y+2和y-x-3的取值,从而去掉绝对值符号化简.
解答:解:(1)∵1+2+3+…+31+32+33=17×33,
∴1-3+2-6+3-9+4-12+…+31-93+32-96+33-99
=(1+2+3+…+33)-(3+6+9+…+99)
=(1+2+3+…+33)-3(1+2+3+…+33)
=-2(1+2+3+…+31+32+33)
=-2×17×33
=-1122;
(2)∵x>0,y<0,
∴x-y+2>0,y-x-3<0,
∴|x-y+2|-|y-x-3|,
=x-y+2+y-x-3,
=-1.
∴1-3+2-6+3-9+4-12+…+31-93+32-96+33-99
=(1+2+3+…+33)-(3+6+9+…+99)
=(1+2+3+…+33)-3(1+2+3+…+33)
=-2(1+2+3+…+31+32+33)
=-2×17×33
=-1122;
(2)∵x>0,y<0,
∴x-y+2>0,y-x-3<0,
∴|x-y+2|-|y-x-3|,
=x-y+2+y-x-3,
=-1.
点评:本题考查的是有理数的混合运算.注意根据题意确定x-y+2和y-x-3的符号以及将所求的式子变形是解此题的关键.

练习册系列答案
相关题目
 如图,△ACD∽△ABC,则下列式子:①CD2=AD•DB;②AC2=AD•AB;③
如图,△ACD∽△ABC,则下列式子:①CD2=AD•DB;②AC2=AD•AB;③| AC |
| CD |
| AB |
| BD |
| A、3个 | B、1个 | C、2个 | D、0个 |
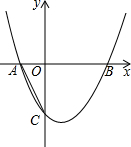 如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点,点A在x轴的负半轴,点B在x轴的正半轴,与y轴交于点C,且CO=2AO,CO=BO,AB=3.则下列判断中正确的是( )
如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点,点A在x轴的负半轴,点B在x轴的正半轴,与y轴交于点C,且CO=2AO,CO=BO,AB=3.则下列判断中正确的是( )| A、此抛物线的解析式为y=x2+x-2 | ||
| B、当x>0时,y随着x的增大而增大 | ||
C、此抛物线与直线y=-
| ||
| D、在此抛物线上的某点M,使△MAB的面积等于4,这样的点共有三个 |
 如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为
如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为