题目内容
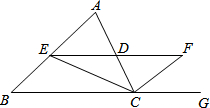如图，在△ABC中，CE、CF分别平分∠ACB和△ACB的外角∠ACG，EF∥BC交AC于点D，求证：DE=DF．考点：等腰三角形的判定与性质,平行线的性质
专题：证明题
分析：利用平行线及角平分线的性质先求得CD=ED，CD=DF，然后等量代换即可证明DE=DF．
解答：证明：∵CE是△ABC的角平分线，
∴∠ACE=∠BCE．
∵CF为外角∠ACG的平分线，
∴∠ACF=∠GCF．
∵EF∥BC，
∴∠GCF=∠F，∠BCE=∠CEF．
∴∠ACE=∠CEF，∠F=∠DCF．
∴CD=ED，CD=DF（等角对等边）．
∴DE=DF．
∴∠ACE=∠BCE．
∵CF为外角∠ACG的平分线，
∴∠ACF=∠GCF．
∵EF∥BC，
∴∠GCF=∠F，∠BCE=∠CEF．
∴∠ACE=∠CEF，∠F=∠DCF．
∴CD=ED，CD=DF（等角对等边）．
∴DE=DF．
点评：本题考查了等腰三角形的判定及角平分线的性质和平行线的性质；进行等量代换是正确解答本题的关键．
练习册系列答案
优生乐园系列答案
相关题目
若有理数a满足|a|=-a，则下列结论正确的是（ ）
| A、a≥0 | B、a≤0 |
| C、a＜-1 | D、-1＜a＜0 |
如图，AB、CD为⊙O的直径，
如图所示，在一块正方形ABCD的布料上要裁出四个大小不同的直角三角形做彩旗，裁剪师傅用画粉在CD边上找出中点F，在BC边上找出点E，使EC=