题目内容
 如图所示,在一块正方形ABCD的布料上要裁出四个大小不同的直角三角形做彩旗,裁剪师傅用画粉在CD边上找出中点F,在BC边上找出点E,使EC=
如图所示,在一块正方形ABCD的布料上要裁出四个大小不同的直角三角形做彩旗,裁剪师傅用画粉在CD边上找出中点F,在BC边上找出点E,使EC=| 1 |
| 4 |
考点:正方形的性质,勾股定理,勾股定理的逆定理
专题:
分析:设正方形的边长为4a,则DF=FC=2a,EC=a.根据勾股定理得出AF2=AD2+DF2=(4a)2+(2a)2=20a2;EF2=(2a)2+a2=5a2;AE2=AB2+BE2=(4a)2+(3a)2=25a2.即可得出AE2=EF2+AF2,由勾股定理逆定理,得∠AFE=90°,从而得出△AFE是直角三角形.
解答:解:方案正确.
理由:设正方形的边长为4a,则DF=FC=2a,EC=a.
在Rt△ADF中,由勾股定理,得AF2=AD2+DF2=(4a)2+(2a)2=20a2;
在Rt△ECF中,EF2=(2a)2+a2=5a2;
在Rt△ABE中,AE2=AB2+BE2=(4a)2+(3a)2=25a2.
∴AE2=EF2+AF2,
∴∠AFE=90°,
∴△AFE是直角三角形.
理由:设正方形的边长为4a,则DF=FC=2a,EC=a.
在Rt△ADF中,由勾股定理,得AF2=AD2+DF2=(4a)2+(2a)2=20a2;
在Rt△ECF中,EF2=(2a)2+a2=5a2;
在Rt△ABE中,AE2=AB2+BE2=(4a)2+(3a)2=25a2.
∴AE2=EF2+AF2,
∴∠AFE=90°,
∴△AFE是直角三角形.
点评:本题考查了勾股定理和勾股定理的逆定理的应用,证得△AFE是直角三角形是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
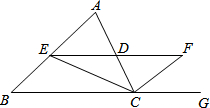 如图,在△ABC中,CE、CF分别平分∠ACB和△ACB的外角∠ACG,EF∥BC交AC于点D,求证:DE=DF.
如图,在△ABC中,CE、CF分别平分∠ACB和△ACB的外角∠ACG,EF∥BC交AC于点D,求证:DE=DF.