题目内容
如图,二次函数的图象与x轴相交于点A(-3,0)、B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx-4k (k≠0)的图象过点P交x轴于点Q.

(1)求该二次函数的解析式;
(2)当点P的坐标为(-4,m)时,求证:∠OPC=∠AQC;
(3)点M、N分别在线段AQ、CQ上,点M以每秒3个单位长度的速度从点A向点Q运动,同时,点N以每秒1个单位长度的速度从点C向点Q运动,当点M、N中有一点到达Q点时,两点同时停止运动,设运动时间为t秒.
①连接AN,当△AMN的面积最大时,求t的值;
②直线PQ能否垂直平分线段MN?若能,请求出此时点P的坐标;若不能,请说明你的理由.
(1)y=x2+4x+3;
(2)见解析;
(3)① ②能,点P的坐标
②能,点P的坐标 或
或
【解析】(1)∵二次函数的图象过点A(-3,0)、B(-1,0),∴设该函数的函数关系式为y=a(x+3)(x+1) ,
又∵函数的图象过点C(0,3),∴3a=3, a=1 ,
∴二次函数的函数关系式为y=(x+3)(x+1),即y=x2+4x+3 ;
(2)∵点P的坐标为(-4,m),∴(-4)2+4×(-4)+3=m,得m=3,则点P的坐标为(-4,3),又点C的坐标为(0,3),∴PC∥OQ , PC=4 ,∵Q是一次函数y=kx-4k的图象与x轴的交点,∴当y=0时,kx-4k=0,即k(x-4)=0
∵k≠0,∴x=4,∴点Q的坐标为(4,0) ,∵PC=OQ=4,∴四边形POQC是平行四边形,∴∠OPC=∠AQC ;
(3)①连结AN,则有AM=3t,CN=t∵点C的坐标为C(0,3), ∴OC=3,由(2)得OQ=4, ∴CQ=5,∴QN=5-t ,过点N作NG⊥AQ于点G,

则△QGN∽△QOC,∴ ,
, ,∴NG=
,∴NG= ,∴△AMN的面积为S与时间t的函数关系式为
,∴△AMN的面积为S与时间t的函数关系式为 即
即 ,
,
∵点M从点A运动到点Q需 秒,点N从点C运动到点Q需5秒,∴点M先到达点Q,即
秒,点N从点C运动到点Q需5秒,∴点M先到达点Q,即 ,∵当
,∵当 时,S随着t的增大而增大,∴当△AMN的面积最大时,
时,S随着t的增大而增大,∴当△AMN的面积最大时,  ,
,
②直线PQ能垂直平分线段MN ,
当NQ=MQ,且PQ与MN的交点H是MN的中点时,PQ垂直平分线段MN,
∵QN=5 -t,MQ=7-3t,则5-t=7-3t, ∴t=1
-t,MQ=7-3t,则5-t=7-3t, ∴t=1
即t =1,且PQ与MN的交点H是MN的中点时,直线PQ垂直平分线段MN,
=1,且PQ与MN的交点H是MN的中点时,直线PQ垂直平分线段MN,
此时NQ=MQ=4,点M的坐标为(0,0)
由①可得 ,
, ,
, ,
,
∴ , ∴点N的坐标为(
, ∴点N的坐标为( ,
, ),∴线段MN的中点H的坐标为(
),∴线段MN的中点H的坐标为( ,
, )
)
∴ ,
,
∴线段MN的垂直平分线段PQ的函数关系式为
∵点P是直线PQ与抛物线y=x2+4x+3的公 共点,∴
共点,∴
解得 ,
, ,
,
∴点P的坐标为 或
或

 D为等边△ABC边BC上的高,AB=4,AE=1,P为高AD上任意一点,则EP+BP的最小值为( )。
D为等边△ABC边BC上的高,AB=4,AE=1,P为高AD上任意一点,则EP+BP的最小值为( )。
 B、
B、 C、
C、 D、
D、

 x2+2x+y-1=0,则x+2y的最大值为 .
x2+2x+y-1=0,则x+2y的最大值为 .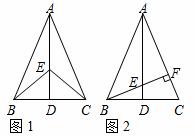
 B.
B.
 D.
D.
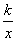 (k≠0)中k的值的变化情况是( )
(k≠0)中k的值的变化情况是( ) 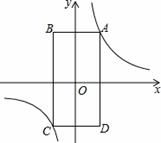

 CD于E, PF
CD于E, PF
 的值为:( )
的值为:( )
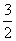 B.3 C.
B.3 C. D.2
D.2