Question

如图1，在△ABC中，AB＝AC，点D是BC的中点，点E在AD上．

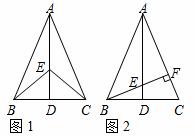
（1）求证：BE＝CE；

（2）若BE的延长线交AC于点F，且BF⊥AC，垂足为F，如图2，∠BAC＝45°，求证：△AEF≌△BCF．

Answer 1

（1）证明见解析；（2）证明见解析．

【解析】（1）∵AB＝AC，D是BC的中点，∴∠BAE＝∠CAE．在△ABE和△ACE中，∵AB＝AC，∠BAE＝∠CAE，AE＝AE，∴△ABE≌△ACE．∴BE＝CE．（运用垂直平分线的性质说明也可）

（2）∵∠BAC＝45°，BF⊥AF，∴△ABF为等腰直角三角形．∴AF＝BF．由（1）知AD⊥BC，∴∠EAF＝∠CBF．在△AEF和△BCF中，AF＝BF，∠AFE＝∠BFC＝90°，∠EAF＝∠CBF，∴△AEF≌△BCF．