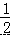题目内容
如图,己知线段 AB=12 厘米,动点 P 以 2 厘米/秒的速度从点 A 出发向点 B 运动,动点 Q 以 4 厘米/秒的速度从点 B 出发向点 A 运动.两点同时出发,到达各自的终点后停止运动.设两点之 间的 距离为 s(厘米),动点 P 的运动时间为 t 秒,则下图中能正确反映 s 与 t 之间的函数关系的是( )
间的 距离为 s(厘米),动点 P 的运动时间为 t 秒,则下图中能正确反映 s 与 t 之间的函数关系的是( )
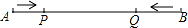
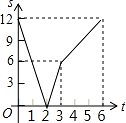
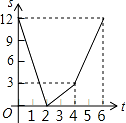 A.
A. 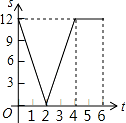 B.
B. 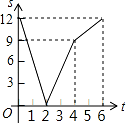 C.
C.
D.
D【考点】动点问题的函数图象.
【专题】函数及其图像.
【分析】根据题意可以得到点 P 运动的慢,点 Q 运动的快,可以算出动点 P 和 Q 相遇时用的时间和 点 B 到达终点时的时间,从而可以解答本题.
【解答】解:设动点 P 和 Q 相遇时用的时间为 x, 12=2x+4x
解得,x=2
此时,点 Q 离开点 B 的距离为:4×2=8cm,点 P 离开点 A 的距离为:2×2=4cm,
相遇后,点 Q 到达终点用的时间为:(12﹣8)÷4=1s,点 P 到达终点用的时间为:(12﹣4)÷2=4s 由上可得,刚开始 P 和 Q 两点间的距离在越来越小直到相遇时,它们之间的距离变为 0,此时用的 时间为 2s;
相遇后,在第 3s 时点 Q 到达终点,从相遇到点 Q 到达终点它们的距离在变大,总的速度与相遇前 总的速度都是两个动点的速度之和;
点 Q 到达终点之后,点 P 继续运动,但是运动的速度相对两个动点同 时运动的速度小,即图象对应 函数图象的倾斜度变小.
时运动的速度小,即图象对应 函数图象的倾斜度变小.
故选 D.
【点评】本题考查动点问题的函数图象,解题的关键是明确各个时间段内它们对应的函数图象.

练习册系列答案
相关题目
 且 x>y,则 2x﹣y 的值为( )
且 x>y,则 2x﹣y 的值为( )