题目内容
3.将一些形状相同的小棒按如图所示的方式摆放.图①中有3根小棒,图②中有9根小棒,图③中有18根小棒.照此规律,图⑧中小棒的根数为( )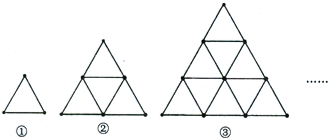
| A. | 84 | B. | 96 | C. | 108 | D. | 118 |
分析 由图可知:第①个图形中有3根火柴棒,第②个图形中有9根火柴棒,第②个图形中有18根火柴棒,…依此类推第n个有1+2+3+…+n个三角形,共有3×(1+2+3+…+n)=$\frac{3}{2}$n(n+1)根火柴;由此代入求得答案即可.
解答 解:∵第①有1个三角形,共有3×1根火柴;
第②个有1+2个三角形,共有3×(1+2)根火柴;
第③个有1+2+3个三角形,共有3×(1+2+3)根火柴;
…
∴第n个有1+2+3+…+n个三角形,共有3×(1+2+3+…+n)=$\frac{3}{2}$n(n+1)根火柴;
∴第⑧个图形中火柴棒根数是3×(1+2+3+4+5+6+7+8)=108.
故选:C.
点评 此题考查了图形的变化规律,解题的关键是发现三角形个数的规律,从而得到火柴棒的根数.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
13.若2x-1=16,则x等于( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
11. 已知AB∥CD,点P是AB上方一点,∠1=60°,∠2=35°,则∠3的度数是( )
已知AB∥CD,点P是AB上方一点,∠1=60°,∠2=35°,则∠3的度数是( )
 已知AB∥CD,点P是AB上方一点,∠1=60°,∠2=35°,则∠3的度数是( )
已知AB∥CD,点P是AB上方一点,∠1=60°,∠2=35°,则∠3的度数是( )| A. | 30° | B. | 35° | C. | 20° | D. | 25° |
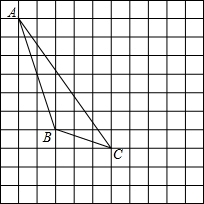 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.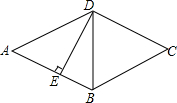 如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,AE:DE=4:3,则下列结论中正确的个数为( )
如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,AE:DE=4:3,则下列结论中正确的个数为( )