题目内容
15.从-2、-1、-$\frac{2}{3}$、0、1这五个数字中,随机抽取一个数,记为a,则使得关于x的方程$\frac{ax+2}{x-3}$=1的解为非负数,且满足关于x的不等式组$\left\{\begin{array}{l}{x-a>0}\\{-3+2x≤1}\end{array}\right.$有三个整数解的概率是$\frac{1}{5}$.分析 首先求得关于x的方程$\frac{ax+2}{x-3}$=1的解为非负数时a的值,满足关于x的不等式组$\left\{\begin{array}{l}{x-a>0}\\{-3+2x≤1}\end{array}\right.$有三个整数解时a的值,再利用概率公式即可求得答案.
解答 解:∵关于x的方程$\frac{ax+2}{x-3}$=1的解为非负数,
∴x=$\frac{5}{1-a}$≥0,
∴1-a>0,
∴a=-2、-1、0;
∵满足关于x的不等式组$\left\{\begin{array}{l}{x-a>0}\\{-3+2x≤1}\end{array}\right.$有三个整数解,
即a<x≤2有三个整数解;
∴-1≤a<0,
∴使得关于x的方程$\frac{ax+2}{x-3}$=1的解为非负数,且满足关于x的不等式组$\left\{\begin{array}{l}{x-a>0}\\{-3+2x≤1}\end{array}\right.$有三个整数解的有2个,当a=-$\frac{2}{3}$时,有增根,
∴使得关于x的方程$\frac{ax+2}{x-3}$=1的解为非负数,且满足关于x的不等式组$\left\{\begin{array}{l}{x-a>0}\\{-3+2x≤1}\end{array}\right.$有三个整数解的概率是:$\frac{1}{5}$.
故答案为:$\frac{1}{5}$.
点评 此题考查了概率公式的应用、分式方程解的情况以及不等式组的解集.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5. 如图,已知a∥b,∠1=65°,则∠2的度数为( )
如图,已知a∥b,∠1=65°,则∠2的度数为( )
 如图,已知a∥b,∠1=65°,则∠2的度数为( )
如图,已知a∥b,∠1=65°,则∠2的度数为( )| A. | 115° | B. | 125° | C. | 65° | D. | 25° |
3.将一些形状相同的小棒按如图所示的方式摆放.图①中有3根小棒,图②中有9根小棒,图③中有18根小棒.照此规律,图⑧中小棒的根数为( )
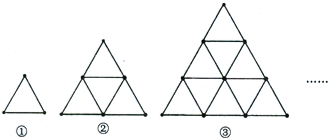

| A. | 84 | B. | 96 | C. | 108 | D. | 118 |
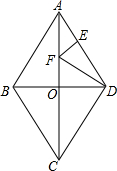 如图,菱形ABCD中,AB=13,BD=10,点O为对角线AC、BD的交点,F是AO上的动点,E是AD边上的动点,则DF+EF的最小值为$\frac{120}{13}$.
如图,菱形ABCD中,AB=13,BD=10,点O为对角线AC、BD的交点,F是AO上的动点,E是AD边上的动点,则DF+EF的最小值为$\frac{120}{13}$.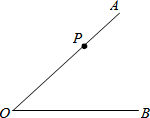 按要求用尺规作图并填空(保留作图痕迹):
按要求用尺规作图并填空(保留作图痕迹):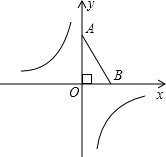 如图,平面直角坐标系中,已知点O(0,0),A(0,2),B(1,0),双曲线y=-$\frac{1}{x}$,动点P在双曲线上,PQ⊥x轴于Q,若△OPQ与△OAB相似,则满足题意的点P一共有($\sqrt{2}$,-$\frac{\sqrt{2}}{2}$)或(-$\sqrt{2}$,$\frac{\sqrt{2}}{2}$)或($\frac{\sqrt{2}}{2}$,-$\sqrt{2}$)或(-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$).
如图,平面直角坐标系中,已知点O(0,0),A(0,2),B(1,0),双曲线y=-$\frac{1}{x}$,动点P在双曲线上,PQ⊥x轴于Q,若△OPQ与△OAB相似,则满足题意的点P一共有($\sqrt{2}$,-$\frac{\sqrt{2}}{2}$)或(-$\sqrt{2}$,$\frac{\sqrt{2}}{2}$)或($\frac{\sqrt{2}}{2}$,-$\sqrt{2}$)或(-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$).