题目内容
矩形ABCD中, 点F在边AD上,过点F作CF⊥EF交AB于点E,AF="CD," 连接BF、CE交于点H,且满足CH=HF+EH.
(1)求证:△AFE≌△DCF.
(2)求证:∠AFE=2∠EFH.)
通过全等三角形的求证规则求证;等边三角形的变换,转化
解析试题分析:证明:(1)∵CF⊥EF
∴
∴ ,且
,且
∴
有知 ,AF=CD,
,AF=CD,
∴△AFE≌△DCF(ASA) 4分
(2) 在矩形ABCD中,有AB=CD
且
∴AB=AF
∴
在线段CH上截取点M,使HM=HF,连接FM。
∵CH=HF+EH
∴FH=HM
∴ ,HM=HF
,HM=HF
且
∴△HFE≌△MFC(AAS)
∴FH=FM
∴FH=FM=HM
∴△HFM为等边三角形
∴
∴
∴
∴∠AFE=2∠EFH
考点:全等三角形的性质和判定
点评:解答本题的关键是熟练掌握判定两个三角形全等的一般方法:SSS、SAS、ASA、AAS、HL,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
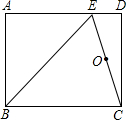 如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
如图,在矩形ABCD中,点E在AD上,EC平分∠BED.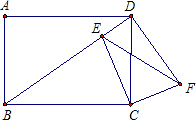 如图,在矩形ABCD中,点E对角线是BD上一点,作∠CEF=∠CBD,过点C作CF⊥CE交EF于F,连接DF.求证:
如图,在矩形ABCD中,点E对角线是BD上一点,作∠CEF=∠CBD,过点C作CF⊥CE交EF于F,连接DF.求证: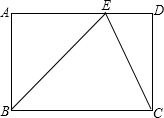 如图,在矩形ABCD中,点E在AD上,CE平分∠BED.
如图,在矩形ABCD中,点E在AD上,CE平分∠BED. (2012•泉港区质检)如图,在矩形ABCD中,点E是BC边上的一动点,DF⊥AE于F,连接DE.
(2012•泉港区质检)如图,在矩形ABCD中,点E是BC边上的一动点,DF⊥AE于F,连接DE.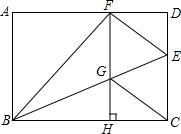 如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.
如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.