题目内容
 (2012•泉港区质检)如图,在矩形ABCD中,点E是BC边上的一动点,DF⊥AE于F,连接DE.
(2012•泉港区质检)如图,在矩形ABCD中,点E是BC边上的一动点,DF⊥AE于F,连接DE.(1)求证:△ABE∽△DFA;
(2)如果AE=BC=10,AB=6,试求出tan∠EDF的值.
分析:(1)由矩形的性质和垂直的定义以及相似三角形的判定方法即可证明:△ABE∽△DFA;
(2)根据相似三角形的对应边比值相等以及勾股定理,可以求得DF,EF的长,运用三角函数定义求解.
(2)根据相似三角形的对应边比值相等以及勾股定理,可以求得DF,EF的长,运用三角函数定义求解.
解答:(1)证明: ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠B=90°,AD∥BC,
∴∠DAE=∠AEB,
∵DF⊥AE于F,
∴∠DFA=∠B=90°,
∴△ABE∽△DFA;
(2)解:∵△ABE∽△DFA;
∴
=
,
∵AE=BC=10,AB=6,
∴在Rt△ABE中,BE=
=8,
∴
=
,
∴AF=8,
∴DF=6,
∴EF=AE-AF=2,
∴tan∠EDF=
=
=
.
 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,∴∠B=90°,AD∥BC,
∴∠DAE=∠AEB,
∵DF⊥AE于F,
∴∠DFA=∠B=90°,
∴△ABE∽△DFA;
(2)解:∵△ABE∽△DFA;
∴
| AD |
| AE |
| AF |
| BE |
∵AE=BC=10,AB=6,
∴在Rt△ABE中,BE=
| AE2-AB2 |
∴
| 10 |
| 10 |
| AF |
| 8 |
∴AF=8,
∴DF=6,
∴EF=AE-AF=2,
∴tan∠EDF=
| EF |
| DF |
| 2 |
| 6 |
| 1 |
| 3 |
点评:本题综合考查了矩形的性质、相似三角形的判定与性质及锐角三角函数的定义.熟练运用矩形的性质和判定,能够找到证明相似三角形的有关条件;运用相似三角形的性质求得三角形中的边,再根据锐角三角函数的概念求解是解题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 (2012•泉港区质检)如图,小刚把一个半径为12cm的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形的纸帽(衔接处无缝隙且不重叠),则圆锥形纸帽的底面圆的半径是
(2012•泉港区质检)如图,小刚把一个半径为12cm的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形的纸帽(衔接处无缝隙且不重叠),则圆锥形纸帽的底面圆的半径是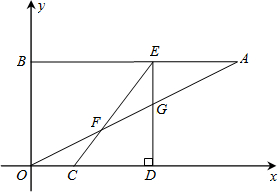
 (2012•泉港区质检)(1)计算:
(2012•泉港区质检)(1)计算: