题目内容
5.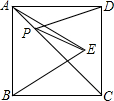 如图,已知正方形ABCD的边长为2,△ABE时等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为2.
如图,已知正方形ABCD的边长为2,△ABE时等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为2.
分析 设AC交BE于P′,连接DP′、PB.四边形ABCD是正方形,B、D关于AC对称,当P与P′重合时,PD+PE=P′E+P′B=BE=2,此时PD+PE的值最小.
解答 解:设AC交BE于P′,连接DP′、PB.
∵四边形ABCD是正方形,
∴B、D关于AC对称,
∴PD=PB,P′D=P′B,
∴PD+PE=PB+PE,
∴当P与P′重合时,PD+PE=P′E+P′B=BE=2,此时PD+PE的值最小,
故答案为2.
点评 本题考查正方形的性质、轴对称的性质、两点之间线段最短等知识,解题的关键是学会利用对称解决最值问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.过n边形的一个顶点画出所有的对角线,可以将这个n边形分成的三角形的个数是( )
| A. | n | B. | n-1 | C. | n-2 | D. | n-3 |
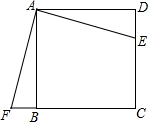 如图,四边形ABCD是正方形,△ABF和△ADE经旋转后得到的,则可知旋转中心为点A,旋转了90度,如果连接EF,那么△AEF是等腰直角三角形.
如图,四边形ABCD是正方形,△ABF和△ADE经旋转后得到的,则可知旋转中心为点A,旋转了90度,如果连接EF,那么△AEF是等腰直角三角形.