题目内容
18．
如图，两个三角形关于某直线对称，则x=（ ）°．| A． | 34 | B． | 35 | C． | 36 | D． | 37 |
分析 根据轴对称的性质可得∠E=∠B，再根据三角形的内角和定理列式计算即可得解．
解答 解：∵两个三角形关于某直线对称，
∴∠E=∠B=117°，
∴x=180°-27°-117°=36°．
故选C．
点评 本题考查轴对称的性质，对应点的连线与对称轴的位置关系是互相垂直，对应点所连的线段被对称轴垂直平分，对称轴上的任何一点到两个对应点之间的距离相等，对应的角、线段都相等．
练习册系列答案
相关题目
8．
如图，直线AB∥CD，AF交CD于点E，∠CEF=135°，则∠A等于（ ）
如图，直线AB∥CD，AF交CD于点E，∠CEF=135°，则∠A等于（ ）| A． | 35° | B． | 40° | C． | 45° | D． | 50° |
9．
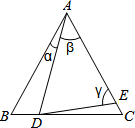如图，D，E分别是△ABC的边BC，AC上的点，若AB=AC，AD=AE，则（ ）
如图，D，E分别是△ABC的边BC，AC上的点，若AB=AC，AD=AE，则（ ）| A． | 当∠β为定值时，∠CDE为定值 | B． | 当∠α为定值时，∠CDE为定值 | ||
| C． | 当∠γ为定值时，∠CDE为定值 | D． | ∠CDE的值与∠α，∠β，∠γ的值无关 |
6．当x=$\sqrt{2}$-1时，代数式x2-1的值是（ ）
| A． | 1 | B． | 2 | C． | 2-$2\sqrt{2}$ | D． | $2\sqrt{2}$-2 |
13．-5的相反数是（ ）
| A． | $-\frac{1}{5}$ | B． | $\frac{1}{5}$ | C． | -5 | D． | 5 |
如图，在平面直角坐标系中，矩形OABC的对角线AC平行于x轴，边OA与x轴正半轴的夹角为30°，OC=4，求点B的坐标．