题目内容
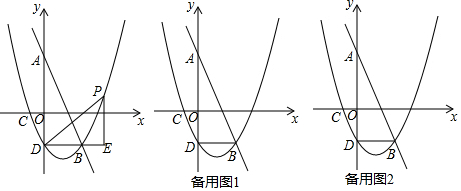
7.如图,直线y=-2x+4交y轴于点A,交抛物线y=$\frac{1}{2}$x2+bx+c于点B(3,-2),抛物线经过点C(-1,0),交y轴于点D,点P是抛物线上的动点,作PE⊥DB交DB所在直线于点E.(1)求抛物线的解析式;
(2)当△PDE为等腰直角三角形时,求出PE的长及P点坐标;
(3)在(2)的条件下,连接PB,将△PBE沿直线AB翻折,直接写出翻折点后E的对称点坐标.
分析 (1)把B(3,-2),C(-1,0)代入y=$\frac{1}{2}$x2+bx+c即可得到结论;
(2)由y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2求得D(0,-2),根据等腰直角三角形的性质得到DE=PE,列方程即可得到结论;
(3)①当P点在直线BD的上方时,如图1,设点E关于直线AB的对称点为E′,过E′作E′H⊥DE于H,求得直线EE′的解析式为y=$\frac{1}{2}$x-$\frac{9}{2}$,设E′(m,$\frac{1}{2}$m-$\frac{9}{2}$),根据勾股定理即可得到结论;②当P点在直线BD的下方时,如图2,设点E关于直线AB的对称点为E′,过E′作E′H⊥DE于H,得到直线EE′的解析式为y=$\frac{1}{2}$x-3,设E′(m,$\frac{1}{2}$m-3),根据勾股定理即可得到结论.
解答 解:(1)把B(3,-2),C(-1,0)代入y=$\frac{1}{2}$x2+bx+c得,$\left\{\begin{array}{l}{-2=\frac{1}{2}×9+3b+c}\\{0=\frac{1}{2}-b+c}\end{array}\right.$,
∴$\left\{\begin{array}{l}{b=-\frac{3}{2}}\\{c=-2}\end{array}\right.$,
∴抛物线的解析式为y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2;
(2)设P(m,$\frac{1}{2}$m2-$\frac{3}{2}$m-2),
在y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2中,当x=0时,y=-2,
∴D(0,-2),
∵B(3,-2),
∴BD∥x轴,
∵PE⊥BD,
∴E(m,-2),
∴DE=m,PE=$\frac{1}{2}$m2-$\frac{3}{2}$m-2+2,或PE=-2-$\frac{1}{2}$m2+$\frac{3}{2}$m+2,
∵△PDE为等腰直角三角形,且∠PED=90°,
∴DE=PE,
∴m=$\frac{1}{2}$m2-$\frac{3}{2}$m,或m=-$\frac{1}{2}$m2+$\frac{3}{2}$m,
解得:m=5,m=1,m=0(不合题意,舍去),
∴PE=5或1,
P(1,-3),或(5,3);
(3)①当P点在直线BD的上方时,如图1,设点E关于直线AB的对称点为E′,
过E′作E′H⊥DE于H,
由(2)知,此时,E(5,-2),
∴DE=5,
∴BE′=BE=2,
∵EE′⊥AB,
∴设直线EE′的解析式为y=$\frac{1}{2}$x+b,
∴-2=$\frac{1}{2}$×5+b,
∴b=-$\frac{9}{2}$,
∴直线EE′的解析式为y=$\frac{1}{2}$x-$\frac{9}{2}$,
设E′(m,$\frac{1}{2}$m-$\frac{9}{2}$),
∴E′H=-2-$\frac{1}{2}$m+$\frac{9}{2}$=$\frac{5}{2}$-$\frac{1}{2}$m,BH=3-m,
∵E′H2+BH2=BE′2,
∴($\frac{5}{2}$-$\frac{1}{2}$m)2+(3-m)2=4,
∴m=$\frac{9}{5}$,m=5(舍去),
∴E′($\frac{9}{5}$,-$\frac{18}{5}$);
②当P点在直线BD的下方时,如图2,设点E关于直线AB的对称点为E′,
过E′作E′H⊥DE于H,
由(2)知,此时,E(1,-2),
∴DE=1,
∴BE′=BE=2,
∵EE′⊥AB,
∴设直线EE′的解析式为y=$\frac{1}{2}$x+b,
∴-2=$\frac{1}{2}$×1+b,
∴b=-$\frac{5}{2}$,
∴直线EE′的解析式为y=$\frac{1}{2}$x-$\frac{5}{2}$,
设E′(m,$\frac{1}{2}$m-$\frac{5}{2}$),
∴E′H=$\frac{1}{2}$m-$\frac{5}{2}$+2=$\frac{1}{2}$m-$\frac{1}{2}$,BH=m-3,
∵E′H2+BH2=BE′2,
∴($\frac{1}{2}$m-$\frac{1}{2}$)2+(m-3)2=4,
∴m=4.2,m=2(舍去),
∴E′(4.2,-0.4),
综上所述,E的对称点坐标为($\frac{9}{5}$,-$\frac{18}{5}$),(4.2,-0.4).
点评 本题考查了待定系数法求二次函数解析式,等腰直角三角形的性质,勾股定理,折叠的性质,正确的作出辅助线是解题的关键.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案| A. | x2+y2 | B. | x2-y | C. | x2-1 | D. | x2+x+1 |
| A. | m>1 | B. | m<2 | C. | -1<m<2 | D. | 1<m<2 |
| A. | (2,-7) | B. | (-4,7) | C. | (4,-7) | D. | (-2,7) |
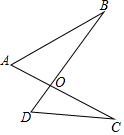 如图,不能判定△AOB和△DOC相似的条件是( )
如图,不能判定△AOB和△DOC相似的条件是( )| A. | AO•CO=BO•DO | B. | $\frac{AO}{DO}=\frac{AB}{CD}$ | C. | ∠A=∠D | D. | ∠B=∠C |
