题目内容
9. 如图,点E、F分别在?ABCD的对角线AC上,且AE=CF,顺次连接点D、E、B、F.
如图,点E、F分别在?ABCD的对角线AC上,且AE=CF,顺次连接点D、E、B、F.(1)求证:四边形DEBF是平行四边形;
(2)请你补充一个条件,当∠DEB=90°时,?DEBF是矩形.
分析 (1)根据平行四边形的判定证明即可;
(2)利用矩形的判定解答即可.
解答 (1)证明:如图,连接BD与AC交于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OA-AE=OC-CF,即OE=OF,
∴四边形DEBF是平行四边形;
(2)当∠DEB=90°或DB=EF时,平行四边形DEBF是矩形.
∵四边形DEBF是平行四边形,
∵∠DEB=90°,
∴平行四边形DEBF是矩形;
故答案为:∠DEB=90°
点评 此题考查平行四边形的判定,关键是根据平行四边形的判定和性质分析解答.

练习册系列答案
相关题目
19.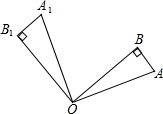 如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )
如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )
 如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )
如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )| A. | 125° | B. | 65° | C. | 75° | D. | 50° |
17.下面是石林县某校八年级(1)班七位女同学的体重(单位:kg):51 50 40 43 48 48 63,这组数据的众数和中位数分别是( )
| A. | 48,43 | B. | 48,48 | C. | 43,48 | D. | 48,49 |
1.函数y=$\frac{\sqrt{x}}{1-x}$的自变量x的取值范围是( )
| A. | x≥0 | B. | x≠1 | C. | x>1 | D. | x≥0且x≠1 |
18.如图所示,用1个边长为c的小正方形和直角边长分别为a,b的4个直角三角形,恰好能拼成一个新的大正方形,其中a,b,c满足等式c2=a2+b2,由此可验证的乘法公式是( )


| A. | a2+2ab+b2=(a+b)2 | B. | a2-2ab+b2=(a-b)2 | C. | (a+b)(a-b)=a2-b2 | D. | a2+b2=(a+b)2 |
19.在平面直角坐标系中,点P(-1,1)位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,直线AB,CD交于点O,OE⊥AB,若∠AOD=50°,则∠COE的度数为40°.
如图,直线AB,CD交于点O,OE⊥AB,若∠AOD=50°,则∠COE的度数为40°.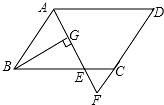 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=4$\sqrt{2}$,求:
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=4$\sqrt{2}$,求: