题目内容
 如图,已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点B处,若∠BDE:∠BED=5:7,则∠B′EC的度数为( )
如图,已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点B处,若∠BDE:∠BED=5:7,则∠B′EC的度数为( )| A、20° | B、30° |
| C、40° | D、50° |
考点:翻折变换(折叠问题),等边三角形的性质
专题:
分析:根据△DEB′是△BDE沿直线DE翻折得到的,得到∠BDE=∠B′DE,∠BED=∠B′ED,∠B=∠B′,结合三角形内角和为180°,以及等边三角形的知识得到∠B′EC的度数.
解答:解:∵△DEB′是△BDE沿直线DE翻折得到的,
∴∠BDE=∠B′DE,∠BED=∠B′ED,∠B=∠B′,
∵△ABC是等边三角形,
∴∠B=∠B′=60°,
∵∠B′DE+∠B′ED+∠B′=180°,
∴∠B′DE+∠B′ED=120°,
∵∠BDE:∠BED=5:7,
∴∠B′ED=∠BED=70°,
∴∠B′EC=180°-∠B′ED-∠BED=180°-140°=40°,
故选C.
∴∠BDE=∠B′DE,∠BED=∠B′ED,∠B=∠B′,
∵△ABC是等边三角形,
∴∠B=∠B′=60°,
∵∠B′DE+∠B′ED+∠B′=180°,
∴∠B′DE+∠B′ED=120°,
∵∠BDE:∠BED=5:7,
∴∠B′ED=∠BED=70°,
∴∠B′EC=180°-∠B′ED-∠BED=180°-140°=40°,
故选C.
点评:本题主要考查了翻折变换问题,得到所求角与所给角的度数的关系是解决本题的关键,此题难度不大.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
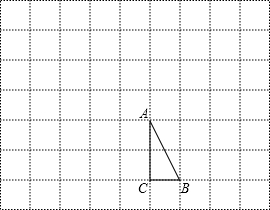 如图在7×9的小正方形网格中,△ABC的顶点A、B、C在网格的格点上,将△ABC向左平移3个单位,再向上平移3个单位得到△A′B′C′,将△ABC按一定规律顺次旋转,第1次将△ABC绕点B顺时针旋转90°得到△A1BC1,第2次将△A1BC1绕点A1顺时针旋转90°得到△A1BC2,第3次将△A1BC2绕点C2顺时针旋转90°得到△A2B2C2,第4次将△A2B2C2绕点B2顺时针旋转90°得到△A3B2C3,依次旋转下去.
如图在7×9的小正方形网格中,△ABC的顶点A、B、C在网格的格点上,将△ABC向左平移3个单位,再向上平移3个单位得到△A′B′C′,将△ABC按一定规律顺次旋转,第1次将△ABC绕点B顺时针旋转90°得到△A1BC1,第2次将△A1BC1绕点A1顺时针旋转90°得到△A1BC2,第3次将△A1BC2绕点C2顺时针旋转90°得到△A2B2C2,第4次将△A2B2C2绕点B2顺时针旋转90°得到△A3B2C3,依次旋转下去. 如图,量一量,算一算.
如图,量一量,算一算. 如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=56°,则∠BCD=
如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=56°,则∠BCD=
 已知圆柱按如图所示方式放置,其左视图的面积为48,则该圆柱的侧面积为
已知圆柱按如图所示方式放置,其左视图的面积为48,则该圆柱的侧面积为 如图,二次函数y=ax2+bx+c的图象与y轴负半轴相交,其顶点为(
如图,二次函数y=ax2+bx+c的图象与y轴负半轴相交,其顶点为(