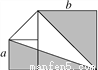
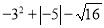题目内容
阅读材料:
小明在学习了二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2 =(1+
=(1+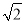 )2.善于思考的小明进行了以下探索:
)2.善于思考的小明进行了以下探索:
设a+b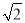 =(m+n
=(m+n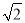 )2(其中a,b,m,n均为正整数),则有a+b
)2(其中a,b,m,n均为正整数),则有a+b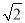 =m2+2n2+2mn
=m2+2n2+2mn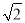 .
.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分形如a+b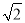 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a,b,m,n均为正整数时,若a+b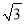 =(m+n
=(m+n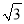 )2,用含m,n的式子分别表示a,b,得a=__________,b=__________;
)2,用含m,n的式子分别表示a,b,得a=__________,b=__________;
(2)利用所探索的结论,找一组正整数a,b,m,n填空:________+________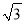 =(________+________
=(________+________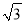 )2;
)2;
(3)若a+4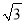 =(m+n
=(m+n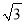 )2,且a,m,n均为正整数,求a的值.
)2,且a,m,n均为正整数,求a的值.
练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
某酒店共有6名员工,所有员工的工资如下表所示:
人 员 | 经理 | 会计 | 厨师 | 服务员1 | 服务员2 | 勤杂工 |
月工资(元) | 6000 | 3000 | 4000 | 2000 | 2000 | 1000 |
(1)酒店所有员工的平均月工资是多少元?中位数、众数各是多少?
(2)平均月工资能准确反映该酒店员工工资的一般水平吗?若能,请说明理由.若不能,如何才能较准确地反映该酒店员工工资的一般水平?谈谈你的看法.
(1)平均月工3000(元),众数为2000元,中位数2500元; (2)这组数据的众数是2000元,才能较准确地反映该酒店员工工资的一般水平,原因是它符合多数人的工资水平. 【解析】试题分析:(1)根据平均数的计算公式,直接求出酒店所有员工的平均月工资即可; (2)由平均数的值,可见平均月工资不能准确反映该酒店员工工资的一般水平,反映该酒店员工工资的一般水平的统计量应符合多数人...

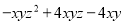 (2)因式分解:
(2)因式分解: 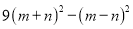
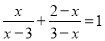
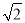 +1)2-
+1)2-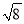 +(-2)2.
+(-2)2.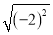 =-2 B. -
=-2 B. -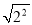 =-2
=-2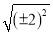 =±2 D.
=±2 D. 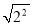 =±2
=±2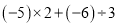 (2)
(2)