题目内容
19. 如图,已知△ABC中,AB=5,AC=3,点D在边AB上,且∠ACD=∠B,则线段AD的长为$\frac{9}{5}$.
如图,已知△ABC中,AB=5,AC=3,点D在边AB上,且∠ACD=∠B,则线段AD的长为$\frac{9}{5}$.
分析 由已知先证△ABC∽△ACD,再根据相似三角形的性质,相似三角形的对应边成比例,即可求出AD的值.
解答 解:∵∠A=∠A,
∠ACD=∠B,
∴△ABC∽△ACD,
∴$\frac{AB}{AC}$=$\frac{AC}{AD}$,
∵AB=5,AC=3,
∴$\frac{5}{3}$=$\frac{3}{AD}$,
∴AD=$\frac{9}{5}$.
故答案为$\frac{9}{5}$.
点评 本题考查相似三角形的判定和性质.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的值.

练习册系列答案
相关题目
9.李明同学手中有五张正面分别画有锐角、线段、等腰三角形、圆、四边形的卡片,卡片的形状、大小和背面花色完全相同.李明随机从手中抽取一张,所抽取的图形不是轴对称图形的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
14.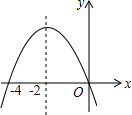 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
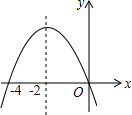 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c<0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )| A. | ①③④ | B. | ②④⑤ | C. | ①②⑤ | D. | ②③⑤ |
11.若关于x的不等式组$\left\{\begin{array}{l}x-m<0\\ 3-2x≤1\end{array}\right.$的所有整数解的和是10,则m的取值范围是( )
| A. | 4<m<5 | B. | 4<m≤5 | C. | 4≤m<5 | D. | 4≤m≤5 |
 关于x的不等式-2x+a≥5的解集如图所示,则a的值是3.
关于x的不等式-2x+a≥5的解集如图所示,则a的值是3.