题目内容
4.为支援灾区,某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同.(1)求A、B两种学习用品的单价各是多少元?
(2)若购买这批学习用品的费用不超过28000元,则最多购买B型学习用品多少件?
分析 (1)设A型学习用品单价x元,利用“用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同”列分式方程求解即可;
(2)设可以购买B型学习用品a件,则A型学习用品(1000-a)件,根据这批学习用品的钱不超过28000元建立不等式求出其解即可.
解答 解:(1)设A型学习用品单价x元,
根据题意得:$\frac{180}{x+10}$=$\frac{120}{x}$,
解得:x=20,
经检验x=20是原方程的根,
x+10=20+10=30.
答:A型学习用品20元,B型学习用品30元;
(2)设可以购买B型学习用品a件,则A型学习用品(1000-a)件,由题意,得:
20(1000-a)+30a≤28000,
解得:a≤800.
答:最多购买B型学习用品800件.
点评 本题考查了列分式方程解应用题和一元一次不等式解实际问题的运用,解答本题时找到等量关系是建立方程的关键.

练习册系列答案
相关题目
12.有大小两种货车,2辆大货车与3辆小货车一次可以运货15.5吨,5辆大货车与6辆小货车一次可以运货35吨.设一辆大货车一次可以运货x吨,一辆小货车一次可以运货y吨,根据题意所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{2x+3y=15.5}\\{5x+6y=35}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+3y=35}\\{5x+6y=15.5}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{3x+2y=15.5}\\{5x+6y=35}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+3y=15.5}\\{6x+5y=35}\end{array}\right.$ |
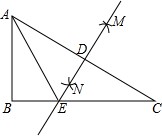 如图,在Rt△ABC中,∠B=90°,分别以点A、点C为圆心,大于$\frac{1}{2}$AC长为半径画弧,两弧相交于点M,N,连结MN,与AC、BC分别交于点D、E,连结AE.
如图,在Rt△ABC中,∠B=90°,分别以点A、点C为圆心,大于$\frac{1}{2}$AC长为半径画弧,两弧相交于点M,N,连结MN,与AC、BC分别交于点D、E,连结AE.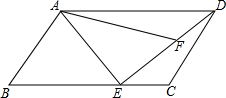 如图所示,在?ABCD中,点E在BC边上,AE=AB,点F在DE上,∠DAF=∠CDE;
如图所示,在?ABCD中,点E在BC边上,AE=AB,点F在DE上,∠DAF=∠CDE; 如图,已知△ABC中,AB=5,AC=3,点D在边AB上,且∠ACD=∠B,则线段AD的长为$\frac{9}{5}$.
如图,已知△ABC中,AB=5,AC=3,点D在边AB上,且∠ACD=∠B,则线段AD的长为$\frac{9}{5}$. 如图,在四边形中ABCD中,AB∥CD,∠1=∠2,DB=DC.
如图,在四边形中ABCD中,AB∥CD,∠1=∠2,DB=DC.