题目内容
10．为了估计池塘中鱼的数量，老张从鱼塘中捕获100条鱼，在每条鱼身上做好记号后把这些鱼放归池塘，过了一段时间，他再从池塘中随机打捞60条鱼，发现其中有15条鱼有记号，则池塘中鱼的条数约为（ ）| A． | 300 | B． | 400 | C． | 600 | D． | 800 |
分析 首先求出有记号的15条鱼在60条鱼中所占的比例，然后根据用样本中有记号的鱼所占的比例等于鱼塘中有记号的鱼所占的比例，即可求得鱼的总条数．
解答 解：由题意可得：100÷$\frac{15}{60}$=400（条）．
答：池塘中鱼的条数约为400条．
故选：C．．
点评 本题考查了统计中用样本估计总体，表示出带记号的鱼所占比例是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．11+101+1001+…+$\underset{\underbrace{10…01}}{99个0}$的和为（ ）
| A． | $\underset{\underbrace{11…1210}}{98个1}$ | B． | $\underset{\underbrace{11…1210}}{99个1}$ | C． | $\underset{\underbrace{11…10}}{100个1}$ | D． | $\underset{\underbrace{11…10}}{101个1}$ |
18．按如图的运算程序，能使输出结果为3的x，y的值是（ ）
| A． | x=5，y=-2 | B． | x=3，y=-3 | C． | x=-4，y=2 | D． | x=-3，y=-9 |
5．下列说法正确的是（ ）
| A． | 经过一点有且只有一条直线 | B． | 射线OA=3cm | ||
| C． | 所有连接两点的线中，线段最短 | D． | 延长线段AB到C使AC=BC |
2．下列几何体从正面看、从左面看、从上面看完全相同的是（ ）
| A． |  圆锥 | B． |  长方体 | C． |  圆柱 | D． |  正方体 |
19．
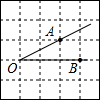如图，在边长为1的小正方形组成的网格中，点A、B、O为格点，则tan∠AOB=（ ）
如图，在边长为1的小正方形组成的网格中，点A、B、O为格点，则tan∠AOB=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{3}$ | C． | $\frac{\sqrt{10}}{5}$ | D． | $\frac{\sqrt{5}}{3}$ |
如图，抛物线y=-x2+bx+c与x轴交于A、B两点（点A在点B的左侧），点A的坐标为（-1，0），与y轴交于点C（0，3），作直线BC．动点P在x轴上运动，过点P作PM⊥x轴，交抛物线于点M，交直线BC于点N，设点P的横坐标为m．