Question

【题目】如图，在中，，，以为项点作等腰直角三角形，使，连接，射线交于点.

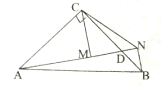
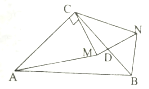
图1 图2

（1）如图1，若点、、在一条直线上，

①求证：；

②若，，求的长；

（2）如图2，若，，将绕点顺时针旋转一周，在旋转过程中射线交于点，当三角形是直角三角形时，请你直接写出的长.

Answer 1

【答案】（1）①见解析，②;（2）或2

【解析】

（1）①如图，过点C作CF⊥CN，交AN于点F，由等腰直角三角形的性质，可求∠CNM=45°，CM=MN，即可证∠FCN=∠ACB，∠CFN=∠CNF=45°，根据“SAS”可证△ACF≌△BCN，可得AF=BN，根据等腰直角三角形的性质可得MF=MN=CM，即可证BN+CM=AM；

②由题意可求出CM=MN=，由全等三角形的性质可得∠CAF=∠CBN，即可证∠MCD=∠CBN，则CM∥BN，可得△MCD∽△NBD，根据相似三角形的性质和勾股定理可求BD的长；

（2）分∠BDH=90°，∠DHB=90°两种情况讨论，根据等腰直角三角形的性质可求CD的长．

证明：（1）①如图，过点C作CF⊥CN，交AN于点F，

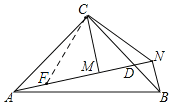
∵△CMN是等腰直角三角形，

∴∠CNM=45°，CM=MN，

∵CF⊥CN，∠ACB=90°，

∴∠FCN=∠ACB，∠CFN=∠CNF=45°，

∴∠ACF=∠BCN，CF=CN，且AC=BC，

∴△ACF≌△BCN（SAS），

∴AF=BN，

∵CF=CN，CM⊥MN，

∴MF=MN=CM，

∴AM=AF+FM=BN+CM；

②∵AM=4，BN=，BN+CM=AM，

∴CM=MN=，

∵△ACF≌△BCN，

∴∠CAF=∠CBN，

∵∠CAF+∠ACF=∠CFN=45°，∠BCN+∠MCD=∠MCN=45°，

∴∠CAF=∠MCD，且∠CAF=∠CBN，

∴∠MCD=∠CBN，

∴CM∥BN，

∴△MCD∽△NBD，∠CMD=∠BND=90°，

∴

∴MD=ND，

∵MD+ND=MN=，

∴ND=，

在Rt△DNB中，BD=，

（2）若∠BDH=90°，如图，此时点M与点D重合，

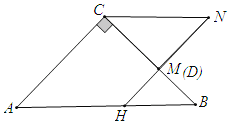
∵△CMN是等腰直角三角形，CN=2，

∴CM=MN=，

∴CD=，

若∠BHD=90°，如图，

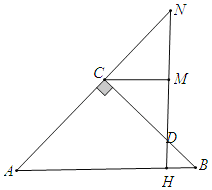
∵∠BHD=90°，∠B=45°，

∴∠BDH=45°，

∴∠CDN=45°=∠N，

∴CD=CN=2．