��Ŀ����
20����ͼ������������y=ax�뷴��������y=$\frac{k}{x}$��x��0����ͼ���ڵ�M��$\sqrt{6}$��$\sqrt{6}$����
��1���������������ı���ʽ��
��2����ͼ1������AMB=90�㣬�������߷ֱ�����������������ύ�ڵ�A��B�����ı���OAMB�������
��3����ͼ2����P�Ƿ���������y=$\frac{k}{x}$��x��0����ͼ����һ�㣬����P��x�ᡢy��Ĵ��ߣ�����ֱ�ΪE��F��PF��ֱ��OM�ڵ�H������x��Ĵ��ߣ�����ΪG�����P�ĺ�����Ϊm����m��$\sqrt{6}$ʱ���Ƿ���ڵ�P��ʹ���ı���PEGHΪ�����Σ������ڣ����P������ꣻ�������ڣ���˵�����ɣ�
���� ��1�����ô���ϵ�������ɽ�����⣮
��2������֤����AMC�ա�BMD���Ƴ�S�ı���OCMD=S�ı���OAMB�����ɽ�����⣮
��3����P��������x��$\frac{6}{x}$������PE=HG=GE=$\frac{6}{x}$��OE=x��
��� �⣺��1������M��$\sqrt{6}$��$\sqrt{6}$���ֱ����y=ax��y=$\frac{k}{x}$�ã�
$\sqrt{6}$=a$\sqrt{6}$��$\sqrt{6}$=$\frac{k}{\sqrt{6}}$��
��ã�a=1��k=6��
�������������ı���ʽ�ֱ�Ϊ��y=x��y=$\frac{6}{x}$��
��2����ͼ1�У�����M�ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪC��D��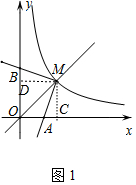
���MCA=��MDB=90�㣬��AMC=��BMD=90��-��AMD��MC=MD=$\sqrt{6}$��
���AMC�ա�BMD��
��S�ı���OCMD=S�ı���OAMB=6��
��3����P��������x��$\frac{6}{x}$������PE=HG=GE=$\frac{6}{x}$��OE=x��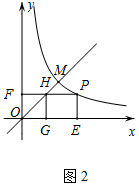
�ߡ�MOE=45�㣬
��OG=GH=$\frac{6}{x}$��
��OE=OG+GH=$\frac{12}{x}$��
��x=$\frac{12}{x}$��
���x=2$\sqrt{3}$��
��P��������2$\sqrt{3}$��$\sqrt{3}$����
���� ���⿼�鷴���������ۺ��⡢������������Ӧ�á�ȫ�������ε��ж������ʡ������ε����ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����Ӹ����߹���ȫ�������ν�����⣬ѧ�����ò����������̽�����⣬�����п���ѹ���⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� |  �ȱ������� | B�� |  ƽ���ı��� | C�� |  �������� | D�� |  ����� |
| A�� |  | B�� |  | C�� |  | D�� |  |
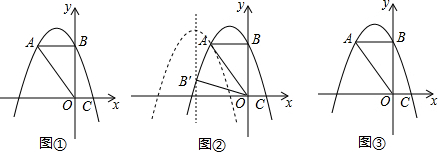
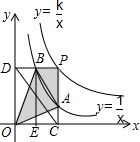 ��������������y=$\frac{k}{x}$��k��1����y=$\frac{1}{x}$�ڵ�һ�����ڵ�ͼ����ͼ��ʾ����P��y=$\frac{k}{x}$����ͼ���ϣ�PC��x���ڵ�C����y=$\frac{1}{x}$��ͼ���ڵ�A��PD��y���ڵ�D����y=$\frac{1}{x}$��ͼ���ڵ�B��BE��x���ڵ�E������P��y=$\frac{k}{x}$����ͼ�����˶�ʱ�����½��ۣ���BA��DCʼ��ƽ�У���PA��PBʼ����ȣ����ı���PAOB��������ᷢ���仯���ܡ�OBA����������ı���
��������������y=$\frac{k}{x}$��k��1����y=$\frac{1}{x}$�ڵ�һ�����ڵ�ͼ����ͼ��ʾ����P��y=$\frac{k}{x}$����ͼ���ϣ�PC��x���ڵ�C����y=$\frac{1}{x}$��ͼ���ڵ�A��PD��y���ڵ�D����y=$\frac{1}{x}$��ͼ���ڵ�B��BE��x���ڵ�E������P��y=$\frac{k}{x}$����ͼ�����˶�ʱ�����½��ۣ���BA��DCʼ��ƽ�У���PA��PBʼ����ȣ����ı���PAOB��������ᷢ���仯���ܡ�OBA����������ı���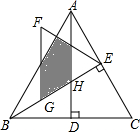 ��ͼ����ABC�ǵȱ������Σ���AD��BE�ཻ�ڵ�H��BC=4����BE�Ͻ�ȡBG=2����GEΪ�����ȱ�������GEF�����ABH���GEF�ص�����Ӱ�����ֵ����Ϊ$\frac{\sqrt{3}}{6}$��
��ͼ����ABC�ǵȱ������Σ���AD��BE�ཻ�ڵ�H��BC=4����BE�Ͻ�ȡBG=2����GEΪ�����ȱ�������GEF�����ABH���GEF�ص�����Ӱ�����ֵ����Ϊ$\frac{\sqrt{3}}{6}$��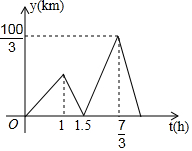 ����ҹ����δ�����죮ɽ��ҹ����������Ǭ¡ʱ�ھ�������������ʱ�ΰ���֪������������Ϊ����ʮ����֮һ���ڳ�������ͷ�����������������������꽭��������������ҹ����һ��������Ŀ��һ���ִ��ӳ�������ͷ����������ʻ��1Сʱ��һ�ҿ�ͧҲ�ӳ�������ͷ������ͬһ��·������ʻ������ͧ�ȵ���Ŀ�ĵغ����̰�ԭ�ٷ��ز���;�����ִ��ڶ������������ִ���ʻ��ʱ��Ϊt��h������ͧ���ִ�֮��ľ���Ϊy��km����y��t�ĺ�����ϵʽ��ͼ��ʾ���ʿ�ͧ���ִ��ڶ�������ʱ����������ͷ�ľ���Ϊ55ǧ�ף�
����ҹ����δ�����죮ɽ��ҹ����������Ǭ¡ʱ�ھ�������������ʱ�ΰ���֪������������Ϊ����ʮ����֮һ���ڳ�������ͷ�����������������������꽭��������������ҹ����һ��������Ŀ��һ���ִ��ӳ�������ͷ����������ʻ��1Сʱ��һ�ҿ�ͧҲ�ӳ�������ͷ������ͬһ��·������ʻ������ͧ�ȵ���Ŀ�ĵغ����̰�ԭ�ٷ��ز���;�����ִ��ڶ������������ִ���ʻ��ʱ��Ϊt��h������ͧ���ִ�֮��ľ���Ϊy��km����y��t�ĺ�����ϵʽ��ͼ��ʾ���ʿ�ͧ���ִ��ڶ�������ʱ����������ͷ�ľ���Ϊ55ǧ�ף�