题目内容
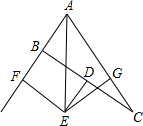 已知,AE平分∠FAC,EF⊥AF,∠AGE=90°,DE是BC垂直平分线,求证:BF=CG.
已知,AE平分∠FAC,EF⊥AF,∠AGE=90°,DE是BC垂直平分线,求证:BF=CG.考点:全等三角形的判定与性质,角平分线的性质,线段垂直平分线的性质
专题:证明题
分析:根据角平分线的性质可以证得EF=EG,然后根据线段的垂直平分线的性质证得BE=EC,则可以证明直角△BEF≌直角△CEG,根据全等三角形的对应边相等证明.
解答: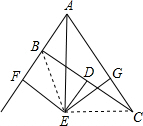 证明:∵AE平分∠FAC,EF⊥AF,∠AGE=90°,即EG⊥AC,
证明:∵AE平分∠FAC,EF⊥AF,∠AGE=90°,即EG⊥AC,
∴EF=EG.
∵DE是BC垂直平分线,
∴BE=EC,
在直角△BEF和直角△CEG中,
,
∴直角△BEF≌直角△CEG,
∴BF=CG.
 证明:∵AE平分∠FAC,EF⊥AF,∠AGE=90°,即EG⊥AC,
证明:∵AE平分∠FAC,EF⊥AF,∠AGE=90°,即EG⊥AC,∴EF=EG.
∵DE是BC垂直平分线,
∴BE=EC,
在直角△BEF和直角△CEG中,
|
∴直角△BEF≌直角△CEG,
∴BF=CG.
点评:本题考查了角平分线的性质,线段的垂直平分线的性质,以及全等三角形的判定与性质,正确作出辅助线,构造全等的三角形是关键.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,AB=18,点C、D在⊙O上,且AC=CD=6,求弦BD的长.
如图,AB是⊙O的直径,AB=18,点C、D在⊙O上,且AC=CD=6,求弦BD的长. 如图,在Rt△ABC中,∠C=90°,∠A=30°,斜边AB=2,求:
如图,在Rt△ABC中,∠C=90°,∠A=30°,斜边AB=2,求: 如图所示,线段AD与BC相交,∠ADC与∠ABC的角平分线相交于O,若∠A=32°,∠C=48°,求∠O的度数.
如图所示,线段AD与BC相交,∠ADC与∠ABC的角平分线相交于O,若∠A=32°,∠C=48°,求∠O的度数. 在下列四个条件中:①AB=DC;②BE=CE;③∠B=∠C;④∠BAE=∠CDE.请选出两个作为条件,得出AE=DE(写出一种即可),并加以证明.
在下列四个条件中:①AB=DC;②BE=CE;③∠B=∠C;④∠BAE=∠CDE.请选出两个作为条件,得出AE=DE(写出一种即可),并加以证明.