题目内容
关于x的不等式ax2-(a2+1)x+a>0(a≠0)的解集为 .
.
.
考点:一元二次不等式
专题:
分析:先将关于x的不等式ax2-(a2+1)x+a>0(a≠0)化为(ax-1)(x-a)>0,再对参数a的取值范围进行讨论,分类解不等式.
解答:解:关于x的不等式ax2-(a2+1)x+a>0(a≠0)化为(ax-1)(x-a)>0,
当(ax-1)(x-a)=0,x1=
,x2=a,
①当a<-1时,原不等式可化为(x-
)(x-a)<0,∵
>a,∴解集为a<x<
;
②当a=-1时,原不等式可化为-(x-1)2>0,解集为空集;
③当-1<a<0时,原不等式可化为(x-
)(x-a)<0,∵a>
,∴解集为
<x<a;
④当0<a<1时,原不等式可化为(x-
)(x-a)>0,∵
>a,∴解集为x<a或x>
;
⑤当a=1时,原不等式可化为(x-1)2>0,解集为x≠1;
⑥当a>1时,原不等式可化为(x-
)(x-a)>0,∵a>
,∴解集为x<
或x>a.
综上所述,关于x的不等式ax2-(a2+1)x+a>0(a≠0)的解集为
.
故答案为:
.
当(ax-1)(x-a)=0,x1=
| 1 |
| a |
①当a<-1时,原不等式可化为(x-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
②当a=-1时,原不等式可化为-(x-1)2>0,解集为空集;
③当-1<a<0时,原不等式可化为(x-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
④当0<a<1时,原不等式可化为(x-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
⑤当a=1时,原不等式可化为(x-1)2>0,解集为x≠1;
⑥当a>1时,原不等式可化为(x-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
综上所述,关于x的不等式ax2-(a2+1)x+a>0(a≠0)的解集为
|
故答案为:
|
点评:考查了一元二次不等式,对a正确分类讨论和熟练掌握一元二次不等式的解法是解题的关键.

练习册系列答案
相关题目
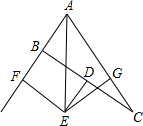 已知,AE平分∠FAC,EF⊥AF,∠AGE=90°,DE是BC垂直平分线,求证:BF=CG.
已知,AE平分∠FAC,EF⊥AF,∠AGE=90°,DE是BC垂直平分线,求证:BF=CG.