题目内容
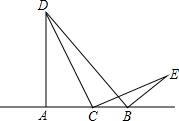 如图,线段AB在直线L上,点C是直线L上一动点.
如图,线段AB在直线L上,点C是直线L上一动点.(1)AD⊥AB,AD=AB,CE⊥CD,BE⊥BD,试判断线段CD和CE的数量关系,并证明;
(2)过点C作CF⊥BD于F,则线段DF、CF、BE之间是否存在某种数量关系,猜想结论并证明.
考点:全等三角形的判定与性质
专题:
分析:(1)过点C作CH⊥AB交BD于H,判断出△BCH是等腰直角三角形,根据等腰直角三角形的性质可得BC=CH,∠CBH=∠CHB=45°,然后求出∠CBE=∠CHD=135°,再根据等角的余角相等求出∠E=∠CDH,然后利用“角角边”证明△BCE和△HCD全等,根据全等三角形对应边相等可得CE=CD;
(2)过点C作CH⊥AB交BD于H,同(1)可得△BCE和△HCD全等,根据全等三角形对应边相等可得DH=BE,再根据等腰直角三角形的性质可得FH=CF,然后根据DF=DH+FH等量代换即可得证;
(2)过点C作CH⊥AB交BD于H,同(1)可得△BCE和△HCD全等,根据全等三角形对应边相等可得DH=BE,再根据等腰直角三角形的性质可得FH=CF,然后根据DF=DH+FH等量代换即可得证;
解答: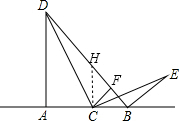 解:(1)如图,过点C作CH⊥AB交BD于H,
解:(1)如图,过点C作CH⊥AB交BD于H,
∵AD⊥AB,AD=AB,
∴△ABD是等腰直角三角形,
∴∠ABD=45°,
∴△BCH是等腰直角三角形,
∴BC=CH,∠CBH=∠CHB=45°,
∵BE⊥BD,
∴∠CBE=∠CHD=135°,
∵CE⊥CD,BE⊥BD,
∴∠E=∠CDH,
在△BCE和△HCD中,
,
∴△BCE≌△HCD(AAS),
∴CE=CD;
(2)DF=BE+CF,
理由:过点C作CH⊥AB交BD于H,同(1)可得△BCE和△HCD全等,
所以DH=BE,
∵△BCH是等腰直角三角形,CF⊥BD,
∴FH=CF,
∵DF=DH+FH,
∴DF=BE+CF.
 解:(1)如图,过点C作CH⊥AB交BD于H,
解:(1)如图,过点C作CH⊥AB交BD于H,∵AD⊥AB,AD=AB,
∴△ABD是等腰直角三角形,
∴∠ABD=45°,
∴△BCH是等腰直角三角形,
∴BC=CH,∠CBH=∠CHB=45°,
∵BE⊥BD,
∴∠CBE=∠CHD=135°,
∵CE⊥CD,BE⊥BD,
∴∠E=∠CDH,
在△BCE和△HCD中,
|
∴△BCE≌△HCD(AAS),
∴CE=CD;
(2)DF=BE+CF,
理由:过点C作CH⊥AB交BD于H,同(1)可得△BCE和△HCD全等,
所以DH=BE,
∵△BCH是等腰直角三角形,CF⊥BD,
∴FH=CF,
∵DF=DH+FH,
∴DF=BE+CF.
点评:本题考查了全等三角形的判定与性质,等腰直角三角形判定与性质,难点在于作辅助线构造出全等三角形和等腰直角三角形,此类题目,各小问的求解思路相同是解题的关键.

练习册系列答案
相关题目
下列式子中,符合代数式的书写规范的是( )
A、3
| ||
B、
| ||
| C、ab÷c | ||
| D、xy×5 |
 如图,△ADE为等边三角形,∠DCE=120°,求证:
如图,△ADE为等边三角形,∠DCE=120°,求证: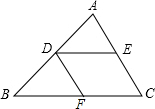 已知:如图,D,E,F分别是△ABC的AB,AC,BC边上的点,DE∥BC,DF∥AC.
已知:如图,D,E,F分别是△ABC的AB,AC,BC边上的点,DE∥BC,DF∥AC.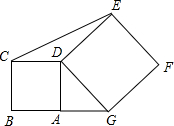 如图,一点A在BG上,四边形ABCD与DEFG都是正方形,其面积分别为7平方厘米,11平方厘米,求△CDE面积.
如图,一点A在BG上,四边形ABCD与DEFG都是正方形,其面积分别为7平方厘米,11平方厘米,求△CDE面积. 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE,F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE,F为AE上一点,且∠BFE=∠C.