题目内容
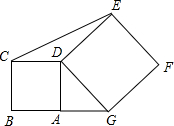 如图,一点A在BG上,四边形ABCD与DEFG都是正方形,其面积分别为7平方厘米,11平方厘米,求△CDE面积.
如图,一点A在BG上,四边形ABCD与DEFG都是正方形,其面积分别为7平方厘米,11平方厘米,求△CDE面积.考点:全等三角形的判定与性质
专题:
分析:过E作EH⊥CD,易证∠ADG=∠EDH,可证△ADG≌△EDH,可得HE=AG,RT△ADG中,易求AG的长度,即可求得△CDE的面积,即可解题.
解答:解:过E作EH⊥CD,
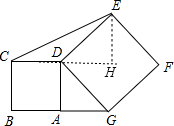
∵∠ADG+∠GDH=90°,∠EDH+∠GDH=90°,
∴∠ADG=∠EDH,
在△ADG和△EDH中,
,
∴△ADG≌△EDH(AAS)
∴HE=AG,
∵四边形ABCD与DEFG都是正方形,其面积分别为7平方厘米,11平方厘米,即AD2=7平方厘米,DG2=11平方厘米,
∴AG=DG2-AD2=
=2厘米,
∴S△CDE=
CD•EH=
平方厘米.

∵∠ADG+∠GDH=90°,∠EDH+∠GDH=90°,
∴∠ADG=∠EDH,
在△ADG和△EDH中,
|
∴△ADG≌△EDH(AAS)
∴HE=AG,
∵四边形ABCD与DEFG都是正方形,其面积分别为7平方厘米,11平方厘米,即AD2=7平方厘米,DG2=11平方厘米,
∴AG=DG2-AD2=
| 11-7 |
∴S△CDE=
| 1 |
| 2 |
| 7 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ADG≌△EDH是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
多项式1+2xy-3xy2的最高次项的系数是( )
| A、1 | B、2 | C、3 | D、-3 |
在数轴上有A,B,C,D四点,它们表示的有理数分别是-4
,3
,-
,-3
,则( )
| 1 |
| 2 |
| 1 |
| 4 |
| 5 |
| 8 |
| 1 |
| 4 |
| A、点C是BD的中点 |
| B、点D是AB的中点 |
| C、点C是AD的中点 |
| D、点C是AB的中点 |
 如图,四边形ABCD的对角线AC,BD相交于O,且将这个四边形分成四个三角形,若OA:OC=OB:OD,则下列结论中一定正确的是( )
如图,四边形ABCD的对角线AC,BD相交于O,且将这个四边形分成四个三角形,若OA:OC=OB:OD,则下列结论中一定正确的是( )| A、I和II相似 |
| B、I和III相似 |
| C、I和IV相似 |
| D、II和IV相似 |
下列具有相反意义的量是( )
| A、“对”与“错” |
| B、盈利10万元和亏损7万元 |
| C、向东+8米与向西-8米 |
| D、气温零下5度 |
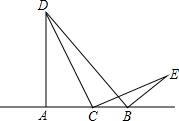 如图,线段AB在直线L上,点C是直线L上一动点.
如图,线段AB在直线L上,点C是直线L上一动点.