题目内容
如图，已知DE平行于BC，AD：DB=1：2，则△ADE与△ABC的面积比为
- A.1：9
- B.1：4
- C.1：2
- D.1：3
A
分析：由DE平行于BC可以得到△ABC∽△ADE，然后利用相似三角形的性质即可求解．
解答：∵DE平行于BC，
∴△ABC∽△ADE，
∴S△ADE：S△ABC=AD2：AB2，
∵AD：DB=1：2，
∴AD：AB=1：3，
∴S△ADE：S△ABC=1：9．
故选A．
点评：此题主要考查了相似三角形的性质与判定，解题时首先根据平行线得到相似三角形，然后利用相似三角形的性质即可求解．
分析：由DE平行于BC可以得到△ABC∽△ADE，然后利用相似三角形的性质即可求解．
解答：∵DE平行于BC，
∴△ABC∽△ADE，
∴S△ADE：S△ABC=AD2：AB2，
∵AD：DB=1：2，
∴AD：AB=1：3，
∴S△ADE：S△ABC=1：9．
故选A．
点评：此题主要考查了相似三角形的性质与判定，解题时首先根据平行线得到相似三角形，然后利用相似三角形的性质即可求解．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
如图，已知在平行四边形ABCD中，对角线AC和BD相交于点O．在BC上取点E，使
4、如图，已知DE平行于BC，AD：DB=1：2，则△ADE与△ABC的面积比为（ ）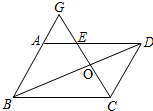
如图：已知在平行四边形ABCD中，E是AD上一点，CE与BD相交于点O，CE与BA的延长线相交于点G，已知DE=2AE，CE=10．