题目内容
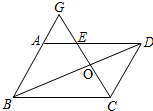如图：已知在平行四边形ABCD中，E是AD上一点，CE与BD相交于点O，CE与BA的延长线相交于点G，已知DE=2AE，CE=10．求GE、CO的长．
分析：由四边形ABCD是平行四边形，即可得BG∥CD，根据平行线分线段成比例定理，即可得
=
，又由DE=2AE，CE=10，即可求得GE的长；又由AD=BC，
=
，即可求得CO的长．
| GE |
| CE |
| AE |
| ED |
| DE |
| BC |
| EO |
| OC |
解答：解：∵四边形ABCD是平行四边形，
∴BG∥CD．（1分）
∴
=
．（1分）
∵DE=2AE，CE=10，
∴
=
．（1分）
∴GE=5．（2分）
由题意知：AD=BC．
∵DE=2AE，
∴
=
．（1分）
又BC∥DE，
∴
=
．（1分）
又EO=EC-OC=10-OC，
∴
=
．（1分）
∴OC=6．（2分）
∴BG∥CD．（1分）
∴
| GE |
| CE |
| AE |
| ED |
∵DE=2AE，CE=10，
∴
| GE |
| 10 |
| AE |
| 2AE |
∴GE=5．（2分）
由题意知：AD=BC．
∵DE=2AE，
∴
| DE |
| BC |
| 2 |
| 3 |
又BC∥DE，
∴
| DE |
| BC |
| EO |
| OC |
又EO=EC-OC=10-OC，
∴
| 2 |
| 3 |
| 10-OC |
| OC |
∴OC=6．（2分）
点评：此题考查了平行四边形的性质与平行线分线段成比例定理．此题图形较复杂，难度适中，解题的关键是注意数形结合思想的应用．
练习册系列答案
相关题目
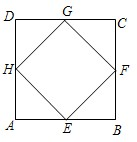四个顶点都在正方形边上的四边形叫做正方形的内接四边形．如图，四边形EFGH是正方形ABCD的内接平行四边形，且已知正方形ABCD的边长为4．
，BO＝AO．又∵AG⊥EB，∠1＋∠3＝
＝∠2＋∠3∴∠1＝∠2，∴Rt△BOE≌Rt△AOF解答此题后某同学产生了如下猜想：对上述命题，若点E在AC的延长线上，AG⊥EB，AG交EB的延长线于G，AG的延长线交DB的延长线于F，其它条件不变，如图，则仍有OE＝OF．问猜想所得的结论是否成立，请说明理由．
