题目内容
如图，已知在平行四边形ABCD中，对角线AC和BD相交于点O．在BC上取点E，使EC=| 1 | 4 |
分析：根据题意作辅助线取DE中点G，连接OG，再根据平行四边形的性质以及EC=
BC，即可得出答案．
| 1 |
| 4 |
解答：
解：取DE中点G，连接OG，
∵四边形ABCD是平行四边形，
∴BO=DO，
∴OG=
BE，OG∥BE，
∵EC=
BC，
∴EC=
BE，
∴EC=
OG．
∵OG∥BC，
∴
=
=
，
∴AO：OF：FC=5：3：2．
解：取DE中点G，连接OG，∵四边形ABCD是平行四边形，
∴BO=DO，
∴OG=
| 1 |
| 2 |
∵EC=
| 1 |
| 4 |
∴EC=
| 1 |
| 3 |
∴EC=
| 2 |
| 3 |
∵OG∥BC，
∴
| CF |
| OF |
| EC |
| OG |
| 2 |
| 3 |
∴AO：OF：FC=5：3：2．
点评：本题主要考查了平行线分线段成比例定理，解题的关键是注意方程思想与数形结合思想的应用，难度适中．
练习册系列答案
阅读快车系列答案
相关题目
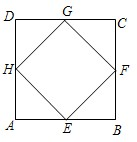四个顶点都在正方形边上的四边形叫做正方形的内接四边形．如图，四边形EFGH是正方形ABCD的内接平行四边形，且已知正方形ABCD的边长为4．
，BO＝AO．又∵AG⊥EB，∠1＋∠3＝
＝∠2＋∠3∴∠1＝∠2，∴Rt△BOE≌Rt△AOF解答此题后某同学产生了如下猜想：对上述命题，若点E在AC的延长线上，AG⊥EB，AG交EB的延长线于G，AG的延长线交DB的延长线于F，其它条件不变，如图，则仍有OE＝OF．问猜想所得的结论是否成立，请说明理由．
