题目内容
19.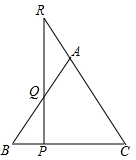 如图,P是等腰三角形ABC底边BC上的一个动点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R.请观察AR与AQ,它们有何关系?并证明你的猜想.
如图,P是等腰三角形ABC底边BC上的一个动点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R.请观察AR与AQ,它们有何关系?并证明你的猜想.
分析 由已知条件,根据等腰三角形两底角相等及三角形两直角互余的性质不难推出∠PRC与∠AQR的关系.
解答  解:AR=AQ,理由如下:
解:AR=AQ,理由如下:
∵AB=AC,
∴∠B=∠C.
∵RP⊥BC,
∴∠B+∠BQP=∠C+∠PRC=90°,
∴∠BQP=∠PRC.
∵∠BQP=∠AQR,
∴∠PRC=∠AQR,
∴AR=AQ.
点评 本题考查了等腰三角形的判定与性质.此题利用“等角对等边”推知AR=AQ的.

练习册系列答案
相关题目
10.已知a,b,c是△ABC的三边长,其中a,b是二元一次方程组$\left\{\begin{array}{l}{a+b=10}\\{2a+b=16}\end{array}\right.$的解,那么c的值可能是下面四个数中的( )
| A. | 2 | B. | 6 | C. | 10 | D. | 18 |
7.计算:-(-1)2015的结果是( )
| A. | 1 | B. | -1 | C. | 2015 | D. | -2015 |
11.已知(x2+y2)2+(x2+y2)=12,那么x2+y2的值是( )
| A. | .3或-4 | B. | .-3或4 | C. | 4 | D. | 3 |