题目内容
9.若a:b:c=5:3:2,则$\frac{a-b+3c}{c}$=4.分析 根据比例的性质,可用c表示a,用c表示b,根据分式的性质,可得答案.
解答 解:由a:b:c=5:3:2,得
a=$\frac{5c}{2}$,b=$\frac{3c}{2}$,
$\frac{a-b+3c}{c}$=$\frac{\frac{5c}{2}-\frac{3c}{2}+3c}{c}$=4,
故答案为:4.
点评 本题考查了比例的性质,利用比例的性质得出a=$\frac{5c}{2}$,b=$\frac{3c}{2}$是解题关键,又利用了分式的性质.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
20.下列计算正确的是( )
| A. | $\sqrt{18}-\sqrt{2}=2\sqrt{2}$ | B. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | C. | $\sqrt{12}÷\sqrt{3}={4}$ | D. | $\sqrt{5}×\sqrt{6}$=$\sqrt{11}$ |
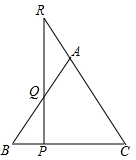 如图,P是等腰三角形ABC底边BC上的一个动点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R.请观察AR与AQ,它们有何关系?并证明你的猜想.
如图,P是等腰三角形ABC底边BC上的一个动点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R.请观察AR与AQ,它们有何关系?并证明你的猜想. 如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.若AB=5,则BD=5$\sqrt{2}$.
如图,AC⊥BC于C,DE⊥AC于E,AD⊥AB于A,BC=AE.若AB=5,则BD=5$\sqrt{2}$. 有一块长方形的土地,宽为120m,建筑商把它分成甲、乙、丙三部分,甲和乙均为正方形,现计划甲建住宅区,乙建商场,丙地开辟成面积为3200m2的公园.若设这块长方形的土地长为xm.那么根据题意列出的方程是x2-360x+32000=0.(将答案写成ax2+bx+c=0(a≠0)的形式)
有一块长方形的土地,宽为120m,建筑商把它分成甲、乙、丙三部分,甲和乙均为正方形,现计划甲建住宅区,乙建商场,丙地开辟成面积为3200m2的公园.若设这块长方形的土地长为xm.那么根据题意列出的方程是x2-360x+32000=0.(将答案写成ax2+bx+c=0(a≠0)的形式)