题目内容
17.关于x的方程:2kx2-(4k+1)x+2k-1=0,当k为何值时方程有两个不相等的实数根?分析 方程有两个不相等实数根,则根的判别式△>0,建立关于k的不等式,求得k的取值范围,且二次项系数不为零.
解答 解:∵方程2kx2-(4k+1)x+2k-1=0,有两个不相等的实数根,
∴△=[-(4k+1)]2-4×2k(2k-1)=16k+1>0,
∴k>-$\frac{1}{16}$,
∴当k>-$\frac{1}{16}$且k≠0时方程有两个不相等的实数根.
点评 本题考查了根的判别式的知识,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
9.在一次“构造勾股数”的探究性学习中,老师给出了下表:
其中m、n为正整数,且m>n.
(1)观察表格,当m=2,n=1时,此时对应的a、b、c的值能否为直角三角形三边的长?说明你的理由.
(2)探究a,b,c与m、n之间的关系并用含m、n的代数式表示:a=m2+n2,b=2mn,c=m2-n2.
(3)以a,b,c为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.
| m | 2 | 3 | 3 | 4 | … |
| n | 1 | 1 | 2 | 3 | … |
| a | 22+12 | 32+12 | 32+22 | 42+32 | … |
| b | 4 | 6 | 12 | 24 | … |
| c | 22-12 | 32-12 | 32-22 | 42-32 | … |
(1)观察表格,当m=2,n=1时,此时对应的a、b、c的值能否为直角三角形三边的长?说明你的理由.
(2)探究a,b,c与m、n之间的关系并用含m、n的代数式表示:a=m2+n2,b=2mn,c=m2-n2.
(3)以a,b,c为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.
 已知A、B在数轴上对应的数分别用a、b表示,且(b+10)2+|a-20|=0,P是数轴上的一个动点.
已知A、B在数轴上对应的数分别用a、b表示,且(b+10)2+|a-20|=0,P是数轴上的一个动点. 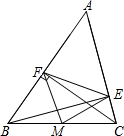 如图,△ABC中,BE⊥AC,CF⊥AB,垂足分别为E、F,M为BC的中点.
如图,△ABC中,BE⊥AC,CF⊥AB,垂足分别为E、F,M为BC的中点.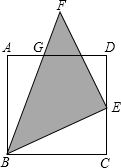 如图,点E是正方形ABCD的CD边上的一点,以BE为一条直角边作等腰直角三角形BEF,斜边BF交AD于G,已知AG=5厘米,GD=15厘米.三角形BEF的面积是272厘米2.
如图,点E是正方形ABCD的CD边上的一点,以BE为一条直角边作等腰直角三角形BEF,斜边BF交AD于G,已知AG=5厘米,GD=15厘米.三角形BEF的面积是272厘米2.