题目内容
12.(1)计算:(3x-y)2-(2x+y)2+5x(y-x)(2)解方程:$\frac{x}{x-2}-1=\frac{8}{{x}^{2}-4}$.
分析 (1)把要求的式子先去掉括号,再合并同类项即可得出答案;
(2)先把分式方程化成整式方程,求出x的值,再进行检验即可得出答案.
解答 解:(1)原式=9x2-6xy+y2-4x2-4xy-y2+5xy-5x2
=(9x2-4x2-5x2)+(-6xy-4xy+5xy)+(y2-y2)
=-5xy;
(2)$\frac{x}{x-2}-1=\frac{8}{{x}^{2}-4}$,
去分母得:x(x+2)-x2+4=8,
去括号得:x2+2x-x2+4=8,
移项合并得:2x=4,
解得:x=2,
经检验x=2是增根,分式方程无解.
点评 此题考查了整式的混合运算和解分式方程,关键是根据整式的混合运算把要求的式子进行化简,把分式方程化成整式方程再求解,注意分式方程一定要检验.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
| 甲种客车 | 乙种客车 | |
| 载客量(座/辆) | 60 | 45 |
| 租金(元/辆) | 550 | 450 |
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
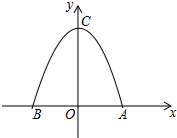 某菜农搭建了一个横截面为抛物线的大棚,建立如图所示的直角坐标系后,抛物线的表达式为y=-$\frac{1}{2}$x2+2.
某菜农搭建了一个横截面为抛物线的大棚,建立如图所示的直角坐标系后,抛物线的表达式为y=-$\frac{1}{2}$x2+2. 如图,C是线段AB的中点,D是线段BC的中点.
如图,C是线段AB的中点,D是线段BC的中点. 如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE∥BC,DE交AF于点G.设AD=10,AB=30,AC=24,GF=12.
如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE∥BC,DE交AF于点G.设AD=10,AB=30,AC=24,GF=12.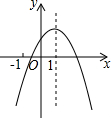 如图,二次函数y=ax2+bx+c的图象的对称轴是直线x=1,则下列结论:
如图,二次函数y=ax2+bx+c的图象的对称轴是直线x=1,则下列结论: