Question

17．如图，直线y=$\frac{1}{5}$x-1与坐标轴交于A、B两点，点P是曲线y=$\frac{k}{x}$（x＞0）上一点，若△PAB是以∠APB=90°的等腰三角形，则k=4．

Answer 1

分析 根据全等三角形的判定与性质，可得AD=BC，DP=CP，根据AD=BC，可得关于x的方程，根据解方程，可得x，根据待定系数法，可得函数解析式．

解答 解：作PC⊥x轴，PD⊥y轴，
如图，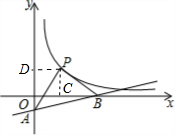
∴∠COD=∠ODM=∠OCM=90°，
∴四边形OCPD是矩形．
在△APD和△BPC中，
$\left\{\begin{array}{l}{∠APD=∠BPC}\\{∠PDA=∠PCB}\\{PA=PB}\end{array}\right.$，
∴△APD≌△BPC（AAS），
∴AD=BC，DP=CP，
∴四边形OCPD是正方形，
∴OC=OD，
∵OA=1，OB=5，
设OD=x，
则AD=x+1，BC=5-x，
∵AD=BC，
∴x+1=5-x，
解得：x=2，
即OD=OC=2，
∴点P的坐标为：（2，2），
∴k=xy=4，
故答案为：4．

点评 本题考查了全等三角形的判定与性质，利用全等三角形的判定与性质得出AD=BC是解题关键，又利用了待定系数法求函数解析式．