题目内容
4. 一幢高层住宅楼发生火灾,消防车立即赶到,在距住宅楼6米的B处升起梯搭在火灾窗口(如图),已知云梯长10米,云梯底部距地面1.8米,发生火灾的住户窗口A离地面有9.8米.
一幢高层住宅楼发生火灾,消防车立即赶到,在距住宅楼6米的B处升起梯搭在火灾窗口(如图),已知云梯长10米,云梯底部距地面1.8米,发生火灾的住户窗口A离地面有9.8米.
分析 根据AB和BC的长度,构造直角三角形,根据勾股定理就可求出直角边AC的长,加上CE的长即可求得AE的长.
解答 解:∵AC⊥BC,
∴∠ACB=90°;
根据勾股定理,得
AC=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴AE=8+1.8=9.8(米);
答:发生火灾的住户窗口距离地面9.8米;
故答案为:9.8.
点评 本题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
15.已知反比例函数y=-$\frac{2}{x}$的图象上有两点A(x1,y1),B(x2,y2),且x1<x2<0,则y1,y2的大小关系为( )
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | 无法确定 |
19.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.点P(-2,1)关于x轴对称的点的坐标为( )
| A. | (2,-1) | B. | (-2,1) | C. | (2,1) | D. | (-2,-1) |
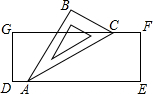 如图,小聪把一块含有30°角的直角三角尺ABC的两个顶点A,C放在长方形纸片DEFG的对边上,若AC平分∠BAE,则∠DAB的度数是120°.
如图,小聪把一块含有30°角的直角三角尺ABC的两个顶点A,C放在长方形纸片DEFG的对边上,若AC平分∠BAE,则∠DAB的度数是120°.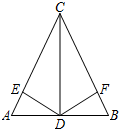 如图,在△ABC中,已知AC=BC,CD平分∠ACB.
如图,在△ABC中,已知AC=BC,CD平分∠ACB.