题目内容
9.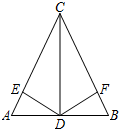 如图,在△ABC中,已知AC=BC,CD平分∠ACB.
如图,在△ABC中,已知AC=BC,CD平分∠ACB.(1)若∠ACD=20°,求∠B的度数;
(2)若点E、F分别在AC、BC边上,且AC=4AE,BC=4BF,求证:DE=DF.
分析 (1)由等腰三角形的性质,得到∠A=∠B,∠ACB=2∠ACD=40°,利用三角形的内角和求出∠B.
(2)证明△ADE≌△BDF,即可得到DE=DF.
解答 解:(1)∵AC=BC,CD平分∠ACB,∠ACD=20°,
∴∠A=∠B,∠ACB=2∠ACD=40°,
∴∠B=(180°-∠ACB)÷2=70°.
(2)∵AC=BC,AC=4AE,BC=4BF,
∴AE=BF,
∵AC=BC,CD平分∠ACB,
∴AD=BD(等腰三角形的三线合一),
在△ADE和△BDF中,
$\left\{\begin{array}{l}{AE=BF}\\{∠A=∠B}\\{AD=BD}\end{array}\right.$,
∴△ADE≌△BDF,
∴DE=DF.
点评 本题考查了等腰三角形的性质、全等三角形的性质与判定,解决本题的关键是熟记等腰三角形的三线合一的性质.

练习册系列答案
相关题目
19.下列说法中正确的是( )
| A. | 若mx=my,则x=y | B. | 若x=y,则$\frac{x}{{m}^{2}}$=$\frac{y}{{m}^{2}}$ | ||
| C. | 若$\frac{x}{m}$=$\frac{y}{m}$,则x=y | D. | 若x2=y2,则x3=y3 |
20.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  等边三角形 | B. |  等腰梯形 | C. |  平行四边形 | D. |  正方形 |
14.下列四个数:-8,-3$\frac{1}{2}$,0.66666…,π,其中无理数的是( )
| A. | -8 | B. | -3$\frac{1}{2}$ | C. | 0.66666… | D. | π |
18.下列各式由左边到右边的变形中,是因式分解的是( )
| A. | (x+2)(x-2)=x2-4 | B. | x2-4y2=(x-2y)(x+2y) | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | 2a(b+c)-3(b+c)=2ab+2ac-3b-3c |
19.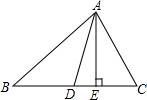 已知AD、AE分别为△ABC的角平分线、高线,若∠B=40°,∠C=60°,则∠ADB的度数为( )
已知AD、AE分别为△ABC的角平分线、高线,若∠B=40°,∠C=60°,则∠ADB的度数为( )
 已知AD、AE分别为△ABC的角平分线、高线,若∠B=40°,∠C=60°,则∠ADB的度数为( )
已知AD、AE分别为△ABC的角平分线、高线,若∠B=40°,∠C=60°,则∠ADB的度数为( )| A. | 115° | B. | 110° | C. | 105° | D. | 100° |
 一幢高层住宅楼发生火灾,消防车立即赶到,在距住宅楼6米的B处升起梯搭在火灾窗口(如图),已知云梯长10米,云梯底部距地面1.8米,发生火灾的住户窗口A离地面有9.8米.
一幢高层住宅楼发生火灾,消防车立即赶到,在距住宅楼6米的B处升起梯搭在火灾窗口(如图),已知云梯长10米,云梯底部距地面1.8米,发生火灾的住户窗口A离地面有9.8米.