题目内容
10．直线y=2x+b被两条坐标轴截得的线段长为5，求该直线与两坐标轴围成的图形的面积．分析 先求出直线y=2x+b与两坐标轴的交点，再根据勾股定理列出关于b的方程，求出b的值即可．
解答 解：当x=0时，y=b，
当y=0时，x=-$\frac{b}{2}$，
则根据勾股定理：b2+（-$\frac{b}{2}$ ）2=52，
解得b=±2$\sqrt{5}$，
故三角形的面积=$\frac{1}{2}$•|b|•|-$\frac{b}{2}$|=5．
点评 本题考查了一次函数图象上点的坐标特征，求出函数与x轴、y轴的交点是解题的关键．
练习册系列答案
相关题目
20．多项式3x2-xy2$-\frac{1}{2}y+1$是（ ）
| A． | 二次四项式 | B． | 三次三项式 | C． | 四次四项式 | D． | 三次四项式 |
1．
如图，直线AB、CD交于点O，OE平分∠AOD，∠AOE=65°，则∠AOC=（ ）
如图，直线AB、CD交于点O，OE平分∠AOD，∠AOE=65°，则∠AOC=（ ）| A． | 20° | B． | 40° | C． | 50° | D． | 80° |
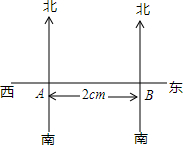如图，某轮船上午8时在A处测得灯塔S在北偏东60°方向上，当轮船继续向东行驶，中午12时到达B处，在B处测得灯塔S在北偏西30°的方向上，已知轮船行驶的速度为20km/h．