题目内容
【题目】如图，点A、B、C、D都在⊙O上，OC⊥AB，∠ADC＝30°.
（1）求∠BOC的度数；
（2）求证：四边形AOBC是菱形.
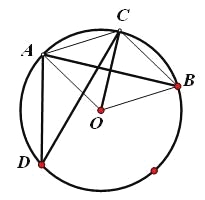
【答案】（1）∠BOC的度数为60°；（2）证明见解析.
【解析】
（1）根据垂径定理得出
，再利用圆周角定理得出∠BOC的度数；
（2）根据等边三角形的判定得出BC=BO=CO，进而利用（1）中结论得出AO=BO=AC=BC，即可证明结论．
(1)∵点A、B、C、D都在⊙O上，OC⊥AB，
∴，
∵∠ADC=30°，
∴∠AOC=∠BOC=2∠ADC=60°，
∴∠BOC的度数为60°；
（2）证明：∵，
∴AC=BC，
AO=BO，
∵∠BOC的度数为60°，BO=CO
∴△BOC为等边三角形，
∴BC=BO=CO，
∴AO=BO=AC=BC，
∴四边形AOBC是菱形．
练习册系列答案
相关题目
